Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét 2 tam giác ABC và A'B'C' bất kì.
Có: \(\overrightarrow{AA'}+\overrightarrow{BB'}+\overrightarrow{CC'}=\left(\overrightarrow{AG}+\overrightarrow{GA'}\right)+\left(\overrightarrow{BG}+\overrightarrow{GB'}\right)+\left(\overrightarrow{CG}+\overrightarrow{GC'}\right)\)
\(=\overrightarrow{0}+\left(\overrightarrow{GA'}+\overrightarrow{GB'}+\overrightarrow{GC'}\right)=3\overrightarrow{GG'}\)
Áp dụng có:
\(\overrightarrow{OO}+\overrightarrow{AC}+\overrightarrow{BD}=3\overrightarrow{GG'}\)
\(\Leftrightarrow\overrightarrow{GG'}=\frac{1}{3}\overrightarrow{AC}+\frac{1}{3}\overrightarrow{BD}\)
#Walker

Bài 1:
H1;H2 lần lượt là trực tâm tam giác OAB, OCD và \(\widehat{AOB}=\widehat{COD}\)(đối đỉnh)
=> \(\frac{OH_1}{OH_2}=\frac{AB}{CD}\)
Gọi M,N,K lần lượt là trung điểm của các đoạn thẳng AD, BC, BD
Vì G1;G2 lần lượt là trọng tâm của các tam giác OAD; OBC. Nên \(\frac{OG_1}{OM}=\frac{2}{3};\frac{OG_2}{ON}=\frac{2}{3}\)
\(\Delta\)OMN có: \(\frac{OG_1}{OM}=\frac{OG_2}{ON}\left(=\frac{2}{3}\right)\)=> G1G2 // MN và \(G_1G_2=\frac{2}{3}MN\)
\(OH_1\perp MK,OH_2\perp NK,MK=\frac{AB}{2},NK=\frac{CD}{2}\)
Do đó: \(\widehat{H_1OH_2}=\widehat{MKN},\frac{OH_1}{MK}=\frac{OH_2}{NK}\). Nên \(\Delta\)OH1H2 đồng dạng với \(\Delta\)KMN (cgc)
=> \(H_1H_2\perp MN\)Mà G1G2 // MN
Nên \(H_1H_2\perp G_1G_2\)=> \(S=\frac{1}{2}H_1H_2\cdot G_1G_2\)
Áp dụng BĐT Cosi cho 2 số dương ta có:
\(S=\frac{1}{2}H_1H_2\cdot G_1G_2=\frac{3G_1G_2\cdot H_1H_2}{6}\le\frac{\left(3G_1G_2+H_1H_2\right)^2}{24}\)
Dấu "=" <=> \(3G_1G_2=H_1H_2\Leftrightarrow OH_1=AB\)và \(OH_2=CD\)
\(\Leftrightarrow\widehat{AOB}=\widehat{COD}=45^o\)
Bài 2: *có nhiều cách làm bài này, mỗi cách có 1 hình khác nhau, đang lỗi nên không vẽ được hình*
Cách 1: Ta có: \(\widehat{BAC}=90^o\)(Góc nội tiếp chắn nửa đường tròn)
Đặt BH=x, ta có HC=HB-BH=2R-x
\(\Delta\)ABC vuông tại A, AH là đường cao
=> AH2=BH.HC. Nên \(AH=\sqrt{x\left(2R-x\right)}\)
Áp dụng BĐT Cosi cho 2 số dương, ta có: AH+BH=\(\sqrt{x\left(2R-x\right)+x}=\frac{1}{\sqrt{3+2\sqrt{2}}}\sqrt{x\left[\left(3+2\sqrt{2}\right)\left(2R-x\right)\right]}+x\)
\(\le\frac{1}{\sqrt{\left(\sqrt{2}+1\right)^2}}\cdot\frac{a+\left(3+2\sqrt{2}\right)\left(2R-x\right)}{2}+x\)\(=\frac{1}{\sqrt{2}+1}\left[\frac{x}{2}\left(\sqrt{2}+1\right)^2\cdot R-\frac{\left(\sqrt{2}+1\right)^2\cdot x}{2}\right]+x\)
\(=\frac{\sqrt{2}-1}{2}\cdot x+\left(\sqrt{2}+1\right)R-\frac{\sqrt{2}+1}{2}x+x=\left(\sqrt{2}+1\right)R\)
Ta có AB+AH \(\le\left(\sqrt{2}+1\right)R\)không đổi
Dấu "=" xảy ra <=> \(x=\left(3+2\sqrt{2}\right)\left(2R-x\right)\)
\(\Leftrightarrow x=\frac{2+\sqrt{2}}{2}R\)
\(\Leftrightarrow\widehat{AOC}=45^o\)
Cách 2: Gọi M là điểm trên nửa đường tròn (O) sao cho \(\widehat{COM}=45^o\) và gọi N là giao của nửa đường tròn (O) tại M với BC
Ta có: M,N cố định; \(\widehat{ONM}=45^o\), BN không đổi
Điểm A trên đường tròn (O)
Do đó tia NA nằm giữa 2 tia NB và NM
\(\Rightarrow\widehat{ANH}\le\widehat{ONM}=45^o\). Mà \(\widehat{ANH}+\widehat{HAN}=90^o\), Nên \(\widehat{HAN}\ge45^o\)
=> \(\widehat{ANH}\le\widehat{HAN},\)\(\Delta\)AHN có: \(\widehat{ANH}\le\widehat{HAN}\Rightarrow AH\le HN\)
Do đó: AH+BH \(\le\)HN+BH=BN, không đổi
Dấu "=" xảy ra <=> A = M
Vậy khi A trên nửa đường tròn (O) sao cho \(\widehat{COA}=45^o\) thì AH+BH lớn nhất

a, Ta có:AM+AN=OM-OA+ON-OA=OM+ON+AC=OC+AC=3/2OC
GA+3GB+GC+OD=2GB+OD=OB+OD=0
C,

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??

a) Ta có: \(\overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} \)\( = 4\overrightarrow {EG} + \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} \)
Mà: \(\overrightarrow {GA} + \overrightarrow {GB} = 2\overrightarrow {GM} ;\) (do M là trung điểm của AB)
\(\overrightarrow {GC} + \overrightarrow {GD} = 2\overrightarrow {GN} \) (do N là trung điểm của CD)
\( \Rightarrow \overrightarrow {EA} + \overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = 4\overrightarrow {EG} + 2(\overrightarrow {GM} + \overrightarrow {GN} ) = 4\overrightarrow {EG} \) (do G là trung điểm của MN)
b) Vì E là trọng tâm tam giác BCD nên \(\overrightarrow {EB} + \overrightarrow {EC} + \overrightarrow {ED} = \overrightarrow 0 \)
Từ ý a ta suy ra \(\overrightarrow {EA} = 4\overrightarrow {EG} \)
c) Ta có: \(\overrightarrow {EA} = 4\overrightarrow {EG} \Leftrightarrow \overrightarrow {EA} = 4.(\overrightarrow {EA} + \overrightarrow {AG} ) \Leftrightarrow - 3\overrightarrow {EA} = 4\overrightarrow {AG} \)
\( \Leftrightarrow 3\overrightarrow {AE} = 4\overrightarrow {AG} \) hay \(\overrightarrow {AG} = \frac{3}{4}\overrightarrow {AE} \)
Suy ra A, G, E thẳng hàng và \(AG = \frac{3}{4}AE \) nên G thuộc đoạn AE.

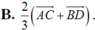
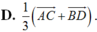
Chọn D.
+ Vì G’ là trọng tâm của tam giác OCD nên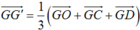 . (1)
. (1)
+ Vì G là trọng tâm của tam giác OAB nên: (2)
(2)
+ Từ (1) và (2) suy ra: