Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
\(MN\perp BC;AB\perp BC\) => MN//AB \(\Rightarrow\frac{MN}{AB}=\frac{CM}{CA}\) (Talet trong tam giác)
\(MP\perp AD;CD\perp AD\) => MP//CD \(\Rightarrow\frac{MP}{CD}=\frac{AM}{CA}\) (Talet trong tam giác)
\(\Rightarrow\frac{MN}{AB}+\frac{MP}{CD}=\frac{CM}{CA}+\frac{AM}{CA}=\frac{CA}{CA}=1\left(dpcm\right)\)

a.
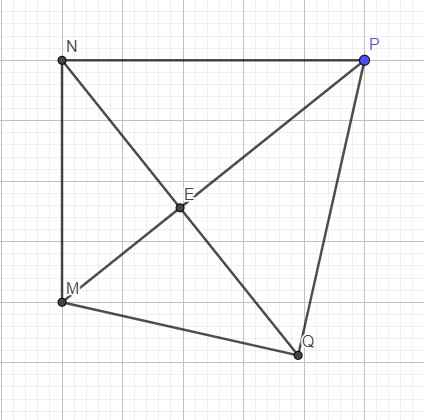
Xét hai tam giác MNP và MQP có:
\(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\\MP\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta MNP=\Delta MQP\left(c.c.c\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{NMP}=\widehat{QMP}\\\widehat{NPM}=\widehat{QPM}\end{matrix}\right.\) hay MP là phân giác của góc M và P
b.
Do \(\left\{{}\begin{matrix}MN=MQ\\NP=PQ\end{matrix}\right.\) \(\Rightarrow MP\) là trung trực NQ
\(\Rightarrow MP\perp NQ\) (đpcm)
Vì\(\hept{\begin{cases}AB\perp BC\left(\widehat{B}=90^0\right)\\MN\perp BC\left(gt\right)\end{cases}\Rightarrow AB//MN}\)( từ vuông góc đến song song )
Xét tam giác ABC có: \(AB//MN\left(cmt\right)\)
\(\Rightarrow\frac{MN}{AB}=\frac{MC}{AC}\)( hệ quả của định lý Ta-let)
Vì \(\hept{\begin{cases}AD\perp DC\left(\widehat{D}=90^0\right)\\MP\perp AD\left(gt\right)\end{cases}\Rightarrow}MP//DC\)( từ vuông góc đến song song )
Xét tam giác ADC có \(MP//DC\left(cmt\right)\)
\(\Rightarrow\frac{MP}{CD}=\frac{AM}{AC}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{MN}{AB}+\frac{MP}{CD}=\frac{MC}{AC}+\frac{AM}{AC}=\frac{AC}{AC}=1\left(đpcm\right)\)