Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

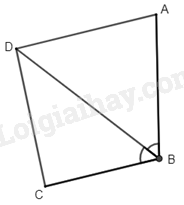
Xét \(\Delta ABD\) ta có: \(AD = AB\) (gt)
\( \Rightarrow \Delta ADB\) cân tại \(A\)
\( \Rightarrow \widehat {ADB} = \widehat {ABD}\)
Mà \(\widehat {ABD} = \widehat {CBD}\) (do \(BD\) là phân giác của góc \(B\))
\( \Rightarrow \widehat {ADB} = \widehat {CBD}\)
Mà hai góc ở vị trí so le trong
\( \Rightarrow AD\;{\rm{//}}\;BC\)
Suy ra \(ABCD\) là hình thang

Xét ▲ADC và ▲BCD có:
AD = BC ( gt )
AC = BD ( gt )
DC chung
=> ▲ADC = ▲BCD ( c.c.c )
=> góc D = góc C ( c.t.ứ )
cmtt ta đc góc A = Góc B
Mà Góc D + góc A + Góc C + Góc B=360o
=> 2GócA+2GócD=360o
-> gócA+gócD=180o ( 2 góc trong cùng phía )=>AB//DC -> ABCD là hình thang
Vì góc D = góc C (cmt) nên ABCD là hình thang cân

a/
Ta có
DC=AD+BC (gt)
CI=BC (gt)
=> DC=AD+CI
Ta có
DC=DI+CI
=> AD=DI => tg ADI cân tại D \(\Rightarrow\widehat{DAI}=\widehat{DIA}\)
Mà \(\widehat{DAI}=\widehat{BAI}\)
\(\Rightarrow\widehat{DIA}=\widehat{BAI}\) Mà 2 góc này ở vị trí so le trong
=> AB//CD => ABCD là hình thang
b/
Ta có
CI=BC (gt) => tg BCI cân tại C \(\Rightarrow\widehat{CBI}=\widehat{CIB}\)
Ta có
AB//CD \(\Rightarrow\widehat{ABI}=\widehat{CIB}\) (góc so le trong)
\(\Rightarrow\widehat{CBI}=\widehat{ABI}\) => BI là phân giác của góc B

tuổi con HN là :
50 : ( 1 + 4 ) = 10 ( tuổi )
tuổi bố HN là :
50 - 10 = 40 ( tuổi )
hiệu của hai bố con ko thay đổi nên hiệu vẫn là 30 tuổi
ta có sơ đồ : bố : |----|----|----|
con : |----| hiệu 30 tuổi
tuổi con khi đó là :
30 : ( 3 - 1 ) = 15 ( tuổi )
số năm mà bố gấp 3 tuổi con là :
15 - 10 = 5 ( năm )
ĐS : 5 năm
mình nha

ta có tam giác BCD cân tại C
=>góc CDB bằng góc CBD
=>BC//AD(goc ADB = gocCBD)
=>DPCM ABCD là hình thang
Học tốt
\(DB\)là phân giác \(\widehat{ADC}\)suy ra \(\widehat{ADB}=\widehat{CDB}\)(1)
\(BC=CD\)suy ra \(\Delta CBD\)cân tại \(C\)suy ra \(\widehat{CBD}=\widehat{CDB}\)(2)
(1)(2) suy ra \(\widehat{ADB}=\widehat{CBD}\)
mà hai góc này ở vị trí so le trong suy ra \(BC//AD\).
Suy ra \(ABCD\)là hình thang.

a. Ta có: AD = AB
=> \(\Delta ABD\) là tam giác cân
=> Góc ADB = góc ABD (1)
Mà góc ABD = góc BDC (so le trong) (2)
Từ (1) và (2), suy ra:
BD là tia phân giác của góc ADC
b. Nối AC
Xét 2 tam giác ABC và ABD có:
AD = BC (gt)
AB chung
=> \(\Delta ABD\sim\Delta ABC\) (1)
Ta có: AD = AB = BC (2)
Từ (1) và (2), suy ra: \(\Delta ABD=\Delta ABC\)
=> Góc A = góc B
Ta có: AB//CD
=> Góc D + góc A = 90o (2 góc trong cùng phía)
Mà góc A = góc B
=> Góc C = góc D
=> ABCD là hình thang cân
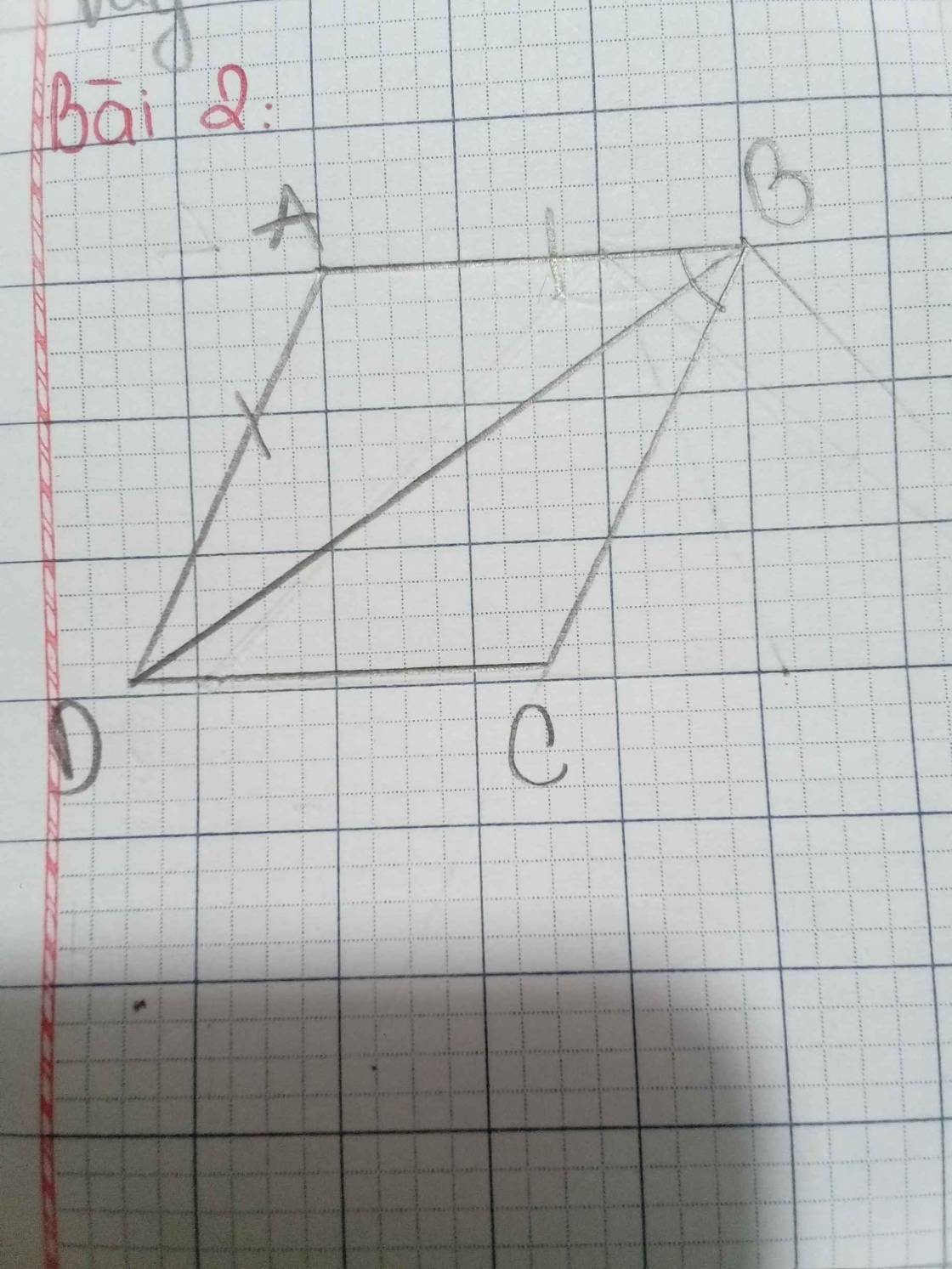


Xét ΔABD có AB=AD
nên ΔABD cân tại A
=>\(\widehat{ABD}=\widehat{ADB}\)
mà \(\widehat{ABD}=\widehat{CBD}\)(BD là phân giác của góc ABC)
nên \(\widehat{ADB}=\widehat{CBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//BC
=>ABCD là hình thang