Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Định chụp hình cơ cơ mà khá khó nhìn nên thoi đánh máy, bạn cố hiểu nhé
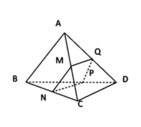
Từ H kẻ đường thẳng song song với ME cắt BC ở K
Từ K kẻ đường thẳng song song với EN cắt CD ở I
Nối I với H ta được mp (P) cần tìm
\(\left\{{}\begin{matrix}K\in HK\subset\left(HKI\right);K\in BC\subset\left(BCD\right)\\I\in KI\subset\left(HKI\right);I\in CD\subset\left(BCD\right)\end{matrix}\right.\Rightarrow\left(HKI\right)\cap\left(BCD\right)=KI\Rightarrow\left(P\right)\cap\left(BCD\right)=KI\)
Ta co \(\left\{{}\begin{matrix}H\in HK\subset\left(HKI\right);H\in AB\subset\left(ABD\right)\\KI//AB\end{matrix}\right.\)
=> Giao tuyen cua (P) va (ABD) la duong thang ua H va song song voi BD

Đáp án C
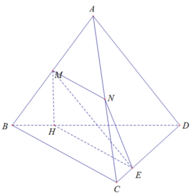
Xét (MNE) và (BCD) có:
E là điểm chung
BC // MN ⇒ BC // (MNE)
⇒ Giao tuyến của 2 mặt phẳng là đường thẳng d đi qua E và song song BC
d cắt BD tại H
⇒ MNEH là thiết diện cần tìm
Xét tứ giác MNEH có MN // EH ( // BC)
⇒ MNEH là hình thang

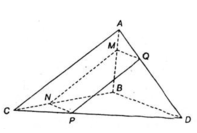
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
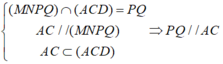
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.

Đáp án B
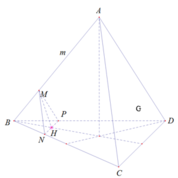
Trong (ABC) kẻ MN // AC ( N ∈ BC)
Trong (ABD) kẻ MP // AD ( P ∈ BD)
⇒ (MNP) là mặt phẳng cần tìm
Xét tam giác MNP có MN = MP =NP (= a - m )
⇒ tam giác MNP đều
Mà NP // CD và BG là trung tuyến tam giác BCD
⇒ BG cắt NP tại H là trung điểm NP
⇒ MH là đường cao tam giác MNP
Ta có: PH = a - m 2 và MP = a – m. Áp dụng định lý pitago, ta có: MH = 3 2 a - m
Và NP = a – m
SMNP = MH . NP 2 = 3 4 a - m 2

Đáp án B

Trong (ABC), kẻ đường thẳng d đi qua M song song CI
d cắt AC tại H
Trong (SAB) kẻ đường thẳng x đi qua M và song song SI
X cắt SA tại J
⇒ (MHJ) là thiết diện cần tìm
Gọi tứ diện đều cạnh 2a ⇒ AI = a
Ta có AM = x và M J S I = A M A I (MJ // SI theo cách dựng)
A M A I = M H C I (MH // CI theo cách dựng)
J H S C = A H A C = A M A I
⇒ MJ = x a . 3 a = x 3
MH = x a . 3 a = x 3
JH = x a . 2 a = 2x
Chu vi thiết diện MHJ là: x 3 + x 3 + 2x = 2x ( 3 + 1 )