Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

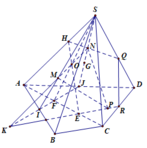
a) Xét (IJK) và (ACD)
có I thuộc (IJK) giao (ACD)
Trong (BCD) vẽ JK cắt CD tại E
=> E thuộc (IJK) giao (ACD) (đoạn này m ghi tắt :D)
Vậy IE là giao tuyến của (IJK) và (ACD)
Ta có E thuộc IE, IE là con của (IJK)
E thuộc CD
=> E là giao điểm của CD với (IJK)
b) Xét (ABD) và (IJK)
K thuộc (ABD) giao (IJK)
=> Kx là giao tuyến của (ABD) và (IJK)
mà AB // IJ
=> Kx // AB
Trong (ABD) vẽ Kx cắt AD tại F
=> F là giao điểm của AD và (IJK)
Ta có Kx // AB và Kx // IJ (cmt)
mà F thuộc Kx
=> KF // IJ

Trong mp (ACD), kéo dài IJ cắt CD tại E thì E là giao điểm của CD và (IJK)

Trong mp(BCD), gọi E là giao điểm của JK và CD
Ta có: \(IE\cap AD=\left\{F\right\}\)
\(IE\subset\left(IJK\right)\)
Do đó: \(AD\cap\left(IJK\right)=F\)
Xét ΔACD có I,F,E thẳng hàng
nên \(\dfrac{AI}{IC}\cdot\dfrac{CE}{ED}\cdot\dfrac{DF}{FA}=1\)
=>\(1\cdot2\cdot\dfrac{DF}{FA}=1\)
=>\(\dfrac{FD}{FA}=\dfrac{1}{2}\)
=>\(\dfrac{FA}{FD}=2\)

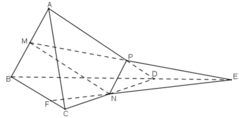
a) Trong mp(ABD): MP không song song với BD nên MP ∩ BD = E.
E ∈ MP ⇒ E ∈ (PMN)
E ∈ BD ⇒ E ∈ (BCD)
⇒ E ∈ (PMN) ∩ (BCD)
Dễ dàng nhận thấy N ∈ (PMN) ∩ (BCD)
⇒ EN = (PMN) ∩ (BCD)
b) Trong mp(BCD) : gọi giao điểm EN và BC là F.
F ∈ EN, mà EN ⊂ (PMN) ⇒ F ∈ (PMN)
⇒ F = (PMN) ∩ BC.