Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo:

a) Tam giác ABD có HK là đường trung bình nên HK//BD
Vì ABCD là hình vuông nên AC⊥BD. Suy ra AC⊥HK
Vì SH⊥(ABCD) nên SH⊥AC
Ta có: AC⊥SH,AC⊥HK nên AC⊥(SHK)
b) Ta có tam giác AHD và tam giác DKC bằng nhau nên DH⊥CK
Mà SH⊥(ABCD) nên SH⊥CK
Suy ra CK⊥(SDH)

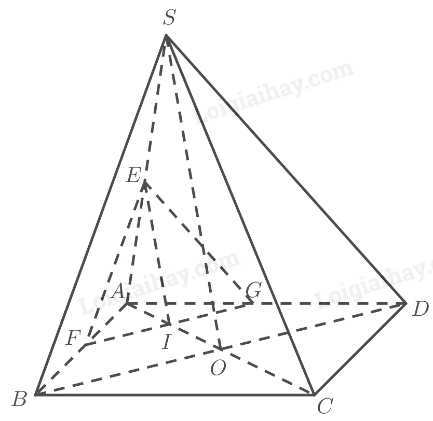
a) \(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(M\) là trung điểm của \(SA\)
\( \Rightarrow OM\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OM\parallel SC\\SC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SBC} \right)\)
\(O\) là trung điểm của \(B{\rm{D}}\) (theo tính chất hình bình hành)
\(N\) là trung điểm của \(SD\)
\( \Rightarrow ON\) là đường trung bình của tam giác \(SB{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow ON\parallel SB\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow ON\parallel \left( {SBC} \right)\)
\(\left. \begin{array}{l}OM\parallel \left( {SBC} \right)\\ON\parallel \left( {SBC} \right)\\OM,ON \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow \left( {OMN} \right)\parallel \left( {SBC} \right)\)
b) \(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(E\) là trung điểm của \(AB\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow OE\parallel \left( {SBC} \right)\)
Do \(\left( {OMN} \right)\parallel \left( {SBC} \right)\) nên \(E \in \left( {OMN} \right)\)
Ta có:
\(\left. \begin{array}{l}EF \subset \left( {OMN} \right)\\\left( {OMN} \right)\parallel \left( {SBC} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {SBC} \right)\)

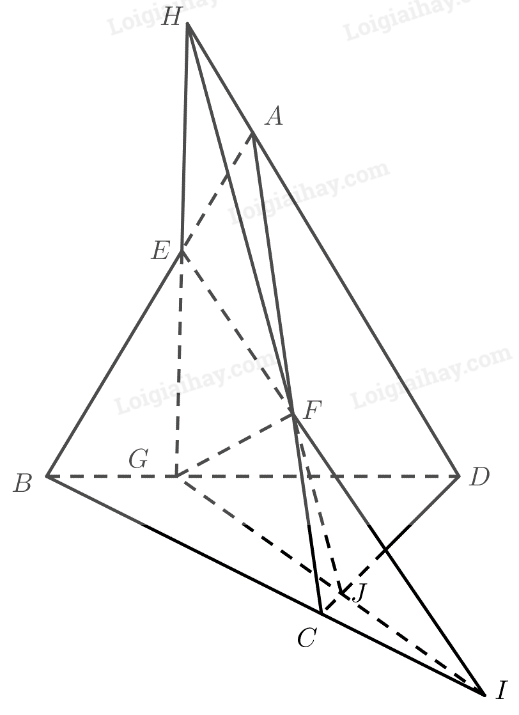
a) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}G \in \left( {EFG} \right)\\G \in BD \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow G \in \left( {EFG} \right) \cap \left( {BCD} \right)\\\left. \begin{array}{l}I \in EF \subset \left( {EFG} \right)\\I \in BC \subset \left( {BCD} \right)\end{array} \right\} \Rightarrow I \in \left( {EFG} \right) \cap \left( {BCD} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {BCD} \right)\) là đường thẳng \(GI\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}F \in \left( {EFG} \right)\\F \in AC \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow F \in \left( {EFG} \right) \cap \left( {ACD} \right)\\\left. \begin{array}{l}H \in EG \subset \left( {EFG} \right)\\H \in A{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow H \in \left( {EFG} \right) \cap \left( {ACD} \right)\end{array}\)
Vậy giao tuyến của hai mặt phẳng \(\left( {EFG} \right)\) và \(\left( {ACD} \right)\) là đường thẳng \(HF\).
b) Gọi \(J\) là giao điểm của \(CD\) và \(IG\).
Ta có:
\(\left. \begin{array}{l}J \in IG \subset \left( {EFG} \right)\\J \in C{\rm{D}} \subset \left( {ACD} \right)\end{array} \right\} \Rightarrow J \in \left( {EFG} \right) \cap \left( {ACD} \right)\)
Mà \(F \in \left( {EFG} \right) \cap \left( {ACD} \right),H \in \left( {EFG} \right) \cap \left( {ACD} \right)\) (theo chứng minh phần a).
Do đó ba điểm \(H,F,J\) thẳng hàng.
Vậy ba đường thẳng \(CD,IG,HF\) cùng đi điểm \(J\).

tham khảo:
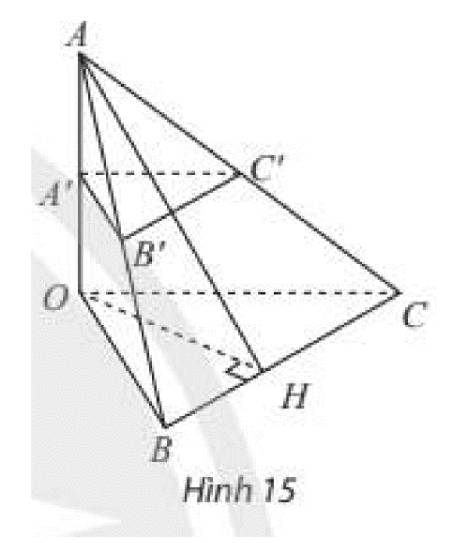
a) Tam giác AOB có A'B' là đường trung bình nên A'B'//AB hay A'B'//(OBC)
Tam giác AOC có A'C' là đường trung bình nên A'C"//AC hay A'C'//(OBC)
Suy ra (A'B'C')//(OBC)
Mà OA⊥(OBC) nên OA⊥(A′B′C′)
b) Vì OA⊥(OBC);BC∈(OBC) nên OA⊥CB
Ta có đường thẳng BC vuông góc với hai đường thẳng OH và OA cắt nhau cùng thuộc (AOH) nên BC⊥(OAH)
Mà tam giác ABC có B'C' là đường trung bình nên B'C'//BC
Suy ra B′C′⊥(AOH)
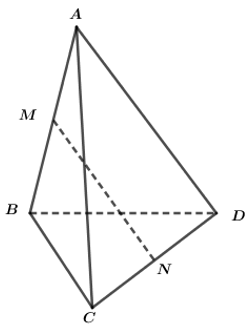


Ta có: \(E\) là trung điểm của \(AB\)
\(F\) là trung điểm của \(AC\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow EF\parallel BC\\BC \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {BC{\rm{D}}} \right)\)
\(E\) là trung điểm của \(AB\)
\(H\) là trung điểm của \(AD\)
\( \Rightarrow EH\) là đường trung bình của tam giác \(ABD\)
\(\left. \begin{array}{l} \Rightarrow EH\parallel BD\\BD \subset \left( {BC{\rm{D}}} \right)\end{array} \right\} \Rightarrow EH\parallel \left( {BC{\rm{D}}} \right)\)
Ta có:
\(\left. \begin{array}{l}EF\parallel \left( {BCD} \right)\\EH\parallel \left( {BCD} \right)\\EF,EH \subset \left( {EFH} \right)\end{array} \right\} \Rightarrow \left( {EFH} \right)\parallel \left( {BCD} \right)\)