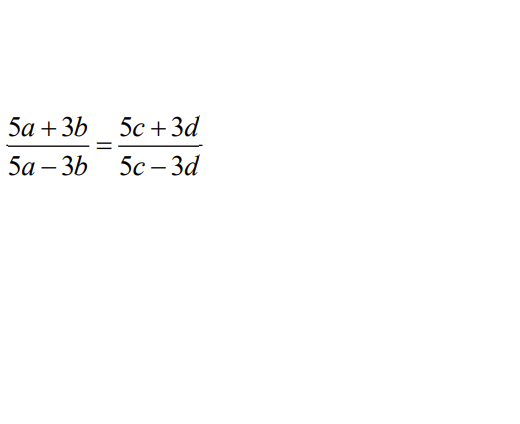NQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
V
1
22 tháng 12 2021
Có \(\frac{a}{b}=\frac{c}{d}=\frac{a}{c}=\frac{b}{d}\)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\)
\(=\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\left(\frac{a+b}{c+d}\right)^2\)
\(=\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\)
Có \(\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Theo dãy tính chất tỉ số bằng nhau ta có :
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\)
Từ (1) và (2) = \(\left(\frac{a+b}{c+d}\right)^2=\frac{a^2+b^2}{c^2+d^2}\)
31 tháng 8 2021
Giải:
Từ \(\frac{ab}{bc}=\frac{b}{c}\left(c\ne0\right)\Rightarrow\frac{ab}{b}=\frac{bc}{c}\left(a,b,c>0\right)\Rightarrow\frac{a}{b}=\frac{b}{c}\)
Tỉ lệ thức \(\frac{a}{b}=\frac{b}{c}\)hay \(ac=b^2\). Ta có: \(\left(a^2+b^2\right)c=\left(a^2+ac\right)=a^2c+ac^2\)
Tương tự có: \(\left(b^2+c^2\right)a=a^2c+ac^2\)
\(\Rightarrow\left(a^2+b^2\right)c=\left(b^2+c^2\right)a\)hay \(\frac{a^2+b^2}{b^2+c^2}=\frac{a}{c}\)
31 tháng 8 2021
1) Áp dụng tính chất của dãy tỉ số = nhau ta có:
ab/bc=b/c=ab−b/bc−c=(10a+b)−b/(10b+c)−c=10a/10b=a/b
⇒a^2/b^2=b^2/c^2=ab/bc=a/c(1)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
a^2/b^2=2=b^2/c^2=a^2+b^2/b^2+c^2(2)
Từ (1) và (2) ⇒a^2+b^2/b^2+c^2=a/c(đpcm)
TT
1
16 tháng 8 2018
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
\(\Rightarrow\hept{\begin{cases}a=bk\\c=dk\end{cases}}\)
\(\Rightarrow\frac{a^2+c^2}{b^2+d^2}=\frac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\frac{\left(b^2.k^2\right)+\left(d^2.k^2\right)}{b^2+d^2}\)
\(=\frac{k^2.\left(b^2+d^2\right)}{b^2+d^2}=k^2\)(1)
và \(\frac{ab}{cd}=\frac{bk.dk}{b.d}=k^2\)(2)
Từ (1) và (2) => \(\frac{a^2+c^2}{b^2+d^2}=\frac{ac}{bd}\)(đpcm)
27 tháng 8 2023
a) \(\dfrac{a}{b}=\dfrac{c}{d}\left(a;b;c;d\ne0\right)\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)
\(\Rightarrow\dfrac{a+b}{b}=\dfrac{c+d}{d}\)
\(\Rightarrow dpcm\)
b) \(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
\(\Rightarrow\dfrac{5a}{5c}=\dfrac{3b}{3d}=\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\)
\(\Rightarrow\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\)
\(\Rightarrow dpcm\)
GR
24 tháng 5 2015
\(\frac{a}{b}=\frac{c}{d}=>\frac{a}{c}=\frac{b}{d}=>\frac{ab}{cd}=\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Áp dụng dãy tỉ số = nhau ta có : \(\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
25 tháng 5 2022
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=kb,=kd\)
\(\Rightarrow\dfrac{5a+3b}{5a-3b}=\dfrac{b\left(5k+3\right)}{b\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\) và \(\dfrac{5c+3d}{5c-3d}=\dfrac{d\left(5k+3\right)}{d\left(5k-3\right)}=\dfrac{5k+3}{5k-3}\)
Vậy \(\dfrac{5a+3b}{5a-3b}=\dfrac{5c+3d}{5c-3d}\)
25 tháng 5 2022
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{5a+3b}{5c+3d}\\\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{5a-3b}{5c-3d}\end{matrix}\right.\)
\(\Rightarrow\dfrac{5a+3b}{5c+3d}=\dfrac{5a-3b}{5c-3d}\Rightarrowđpcm\)
29 tháng 7 2021
a) Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^0\)(Định lí tổng bốn góc trong một tứ giác)
mà \(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}\)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{\widehat{A}}{1}=\dfrac{\widehat{B}}{2}=\dfrac{\widehat{C}}{3}=\dfrac{\widehat{D}}{4}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\dfrac{360^0}{10}=36^0\)
Do đó: \(\widehat{A}=36^0;\widehat{B}=72^0;\widehat{C}=108^0;\widehat{D}=144^0\)
Ta có: \(\widehat{B}+\widehat{C}=180^0\)
mà hai góc này là hai góc trong cùng phía
nên AB//CD(dấu hiệu nhận biết hai đường thẳng song song)
hay ABCD là hình thang