Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hình tự vẽ:
a)Xét tam giác BAD và tam giác BED:
BD:cạnh chung
^ABD=^EBD (vì BD là tia phân giác của ^ABC)
AB=BE(gt)
=>tam giác BAD=tam giác BED(c.g.c)
b)Từ tam giác BAD=tam giác BED(cmt)
=>AD=DE(cặp cạnh t.ứ)
và ^BAD=^BED(cặp góc .tứ),mà ^BAD=900 (^BAC=900)=>^BED=900
Xét tam giác DFA vuông ở A và tam giác DCE vuông ở E có:
AD=AE (cmt)
^ADF=^EDC (2 góc đối đỉnh)
=>tam giác DFA=tam giác DCE(cgv-gnk)
=>DF=DC(cặp cạnh t.ứ)
=>tam giác DFC cân tại D (dấu hiệu nhận biết tam giác cân)
c)Từ tam giác DFA=tam giác DCE (cmt)
=>AF=CE(cặp cạnh t.ứ)
Ta có: BE+CE=BC
BA+AF=BF
mà AF=CE(cmt),AB=AE(gt)
=>BC=BF
=>tam giác BFC cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BCF=\(\frac{180^0-FBC}{2}\) (tính chất tam giác cân) (1)
Vì AB=AE(gt)
=>tam giác ABE cân tại B (dấu hiệu nhận biết tam giác cân)
=>^BEA=\(\frac{180^0-ABE}{2}\) (tính chất tam giác cân) (2)
Từ (1);(2);lại có ^ABE=^FBC
=>^BCF=^BEA,mà 2 góc này nằm ở vị trí đồng vị
=>AE//CF(dấu hiệu nhận biết 2 đg thẳng song song)

Bạn tự vẽ hình nha ^^
a)--- Xét \(\Delta ABD\)và \(\Delta EBD\)có
\(AB=EB\left(GT\right)\)(1)
\(\widehat{BAD}=\widehat{BED}=90^o\)(2)
\(BD:\)Cạnh chung (3)
Từ (1) ;(2) và (3)
\(\Rightarrow\Delta ABD=\Delta EBD\)( c.g.c )
b)
---Theo đề bài ta có :
\(AB=EB\left(GT\right)\)(1)
và \(\widehat{ABC}=60^o\left(gt\right)\)(2)
Từ (1)và (2)\(\Rightarrow\Delta ABE\)đều (đpcm)
--- Vì \(\Delta ABE\)đều
\(\Rightarrow AB=BE=AE\)
Mà \(AB=6cm\)(gt)
...\(AE=EC\)
\(\Rightarrow EC=6cm\)
mà \(BE=6cm\)
Có \(EC+BE=BC\)
\(\Rightarrow6+6=12cm\)
Vậy BC =12cm

a: Xét ΔABE và ΔDBE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔABE=ΔDBE
b: Xét ΔAEF vuông tại A và ΔDEC vuông tại D có
EA=ED
AF=DC
Do đó: ΔAEF=ΔDEC
Suy ra: EF=EC
hay E nằm trên đường trung trực của CF(1)
Ta có: BF=BC
nên B nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra BE là đường trung trực của CF
=>BE⊥CF
hay BG⊥CF

a)xét ΔABE và ΔADE có:
AE là cạnh chung
\(\widehat{DAE}=\widehat{BAE}\)(AE là tia phân giác của \(\widehat{BAD}\))
AD=AB(gt)
⇒ ΔABE=ΔADE(c-g-c)
b)gọi I là giao điểm của AE và BD ta được:
xét ΔADI và ΔABI có:
AI là cạnh chung
\(\widehat{DAI}=\widehat{BAI}\)(AI là tia phân giác của \(\widehat{BAD}\))
AD=AB(gt)
⇒ΔADI=ΔABI(c-g-c)
⇒.ID=IB(2 cạnh tương ứng)(1)
.\(\widehat{DIA}=\widehat{BIA}\)(2 góc tương ứng)(2)
Mà \(\widehat{DIA}+\widehat{BIA}=180^o\)(2 góc kề bù)(3)
Từ (2) và (3) ⇒\(\widehat{DIA}=\widehat{BIA}=\dfrac{180^o}{2}=90^o\)(4)
Từ (1) và (4) ⇒AE là trung trực của BD(đ.p.c.m)
c)xét ΔEBF có:EF là cạnh huyền⇒EF>EB
Mà DE=BE
⇒DE<EF(đ.p.cm)
d)ta có:
vì ΔABE=ΔADE ⇒\(\widehat{EBA}=\widehat{EDA}=90^o\)
xét ΔCDE và ΔFBE có:
\(\widehat{EBF}=\widehat{EDC}=90^o\)
\(\widehat{CED}=\widehat{FEB}\)(2 góc đối đỉnh)
ED=EB( ΔABE=ΔADE)
⇒ ΔCDE=ΔFBE(g-c-g)
⇒CE=EF(2 cạnh tương ứng)
⇒ΔCEF cân tại E
⇒\(\widehat{CFE}=\dfrac{180^o-\widehat{CEF}}{2}\)
vì ΔABE=ΔADE⇒ED=EB(2 cạnh tương ứng)
⇒ΔEDB cân tại E
⇒\(\widehat{EDB}=\dfrac{180^o-\widehat{DEB}}{2}\)
Mà \(\widehat{DEB}=\widehat{CEF}\)(2 góc đối đỉnh)
⇒\(\widehat{CFE}=\widehat{BDE}\)
⇒CF//BD
Mà AG⊥BD
⇒AG⊥CF(đ.p.cm)

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: DA=DE
b: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó:ΔADK=ΔEDC
Suy ra:DK=DC
hay ΔDKC cân tại D
c: BC=10cm
AB=6cm
=>AC=8cm

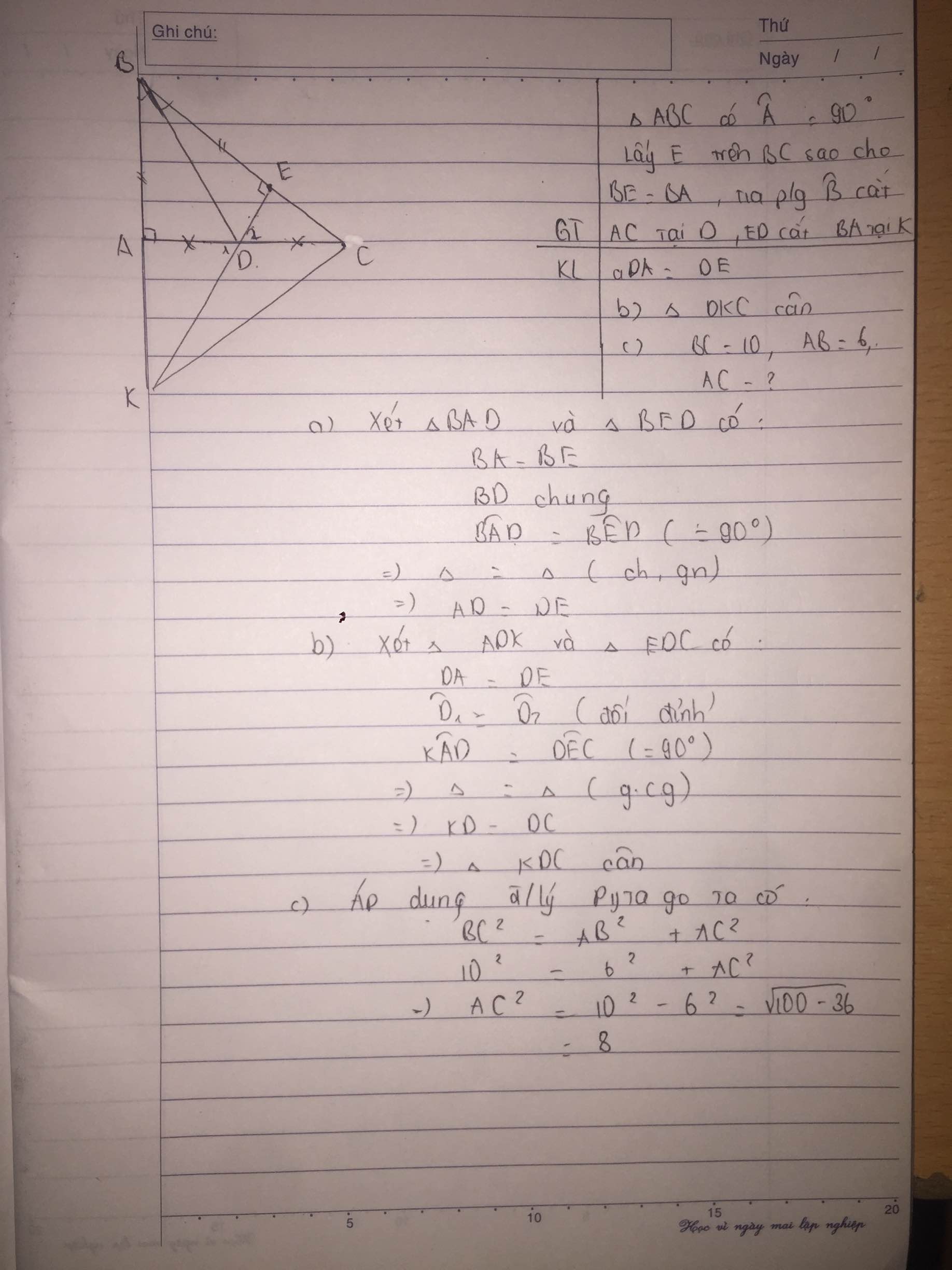
hình tự vẽ
a)Xét tam giác BAD vuông tại A và tam giác BED vuông ở E có:
góc ABD=góc EBD (DE là p/g của góc ABC)
BD : cạnh chung
Suy ra: tam giác BAD = tam giác BED (ch-gn)
=>AD=DE(2 cạnh tương ứng)
b)Ta có: GE là đường cao thứ nhất của tam giác GBC
CA là đường cao thứ 2 của tam giác GBC
Mà GE và CA cắt nhau ở D
=> D là trực tâm
=>BD là đường cao thứ 3 của tam giác GBC
Mà BD cũng là đường p/g của tam giác GBC nên: tam giác GBC cân tại B
=>BG=BC
Mà BC=BF nên \(GB=BC=BF=\frac{1}{2}FC\)
Suy ra: tam giác FGC vuông tại G(Nếu một tam giác có trung tuyến ứng với một cạnh
bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.)