Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Số tập con chứa 3 phần tử lấy từ tập 3 bằng số tổ hợp chập 3 của 20 là C 20 3

Đáp án D
Phương pháp:
Số tập con gồm 5 phần tử của 1 tập hợp gồm 20 phần tử là một tổ hợp chập 5 của 20.
Cách giải: Số tập con gồm 5 phần tử của M là C 20 5 .

Chọn B
Số tập hợp con của A khác rỗng có số phần tử là số chẵn là:
![]()
Để tính M ta xét: ![]()
![]()
Thay x = 1 ta có: ![]()
![]()
Thay x = -1 ta có: ![]()
![]()
Từ (1) và (2) ta có:
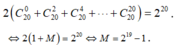

Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.

1/ Số cách chọn 4 học sinh bất kì: \(C_{12}^4\)
Số cách chọn 4 học sinh có mặt đủ 3 lớp:
\(C_5^2.C_4^1.C_3^1+C_5^1.C_4^2.C_3^1+C_5^1.C_4^1.C_3^2\)
Số cách chọn thỏa mãn yêu cầu:
\(C_{12}^4-\left(C_5^2.C_4^1.C_3^1+C_5^1.C_4^2.C_3^1+C_5^1.C_4^1.C_3^2\right)\)
2/ Số tập con có 2 phần tử: \(C_n^2\)
Số tập con có 4 phần tử: \(C_n^4\)
\(C_n^4=20C_n^2\Leftrightarrow\frac{n!}{\left(n-4\right)!.4!}=\frac{20n!}{\left(n-2\right)!.2!}\)
\(\Leftrightarrow\left(n-2\right)\left(n-3\right)=\frac{20.4!}{2!}=240\)
\(\Leftrightarrow n^2-5n-234=0\Rightarrow n=18\)
3/ Từ 10 chữ số {0;1;...;9} có \(C_{10}^3\) cách chọn bộ 3 số tự nhiên phân biệt
Với mỗi bộ số có duy nhất 1 cách sắp xếp thỏa mãn \(a>b>c\)
Vậy có \(C_{10}^3\) chữ số thỏa mãn

Chọn A
Lời giải.
Số tập hợp con khác rỗng có số phần từ chẵn là số cách chọn số phần tử chẵn từ 20 phần tử
Do đó số tập con là
![]()
Tính tổng trên bằng cách khai triển nhị thức Niutơn hoặc dùng máy tính cầm tay và đối chiếu các đáp án

Đáp án C
Phương pháp: Sử dụng công thức tổ hợp chập của phần tử trong khi chọn các tập hợp con có 2,4,6,…,20 phần tử.
Cách giải:
*TH1: A có 2 phần tử => có C 20 2 tập hợp con có 2 phần tử.
*TH2: A có 4 phần tử => có C 20 4 tập hợp con có 4 phần tử.
….
*TH10: A có 20 phần tử => có C 20 20 tập hợp con có 20 phần tử.
Suy ra tất cả có ∑ i = 1 10 C 20 2 i = 2 19 - 1 trường hợp.

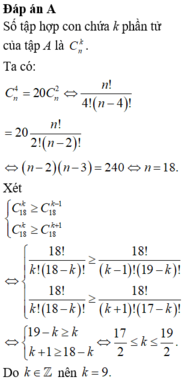
Đáp án C
Phương pháp: Sử dụng tổ hợp chập 3 của 20 để lấy ra 3 phần tử trong tập 20 phần tử.
Cách giải: Số tập con gồm 3 phần tử của S là C 20 3