Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Nếu tập hợp A có n phần tử , k là số tự nhiên nhỏ hơn hoặc bằng n. Tìm số tập con của A có k phần tử


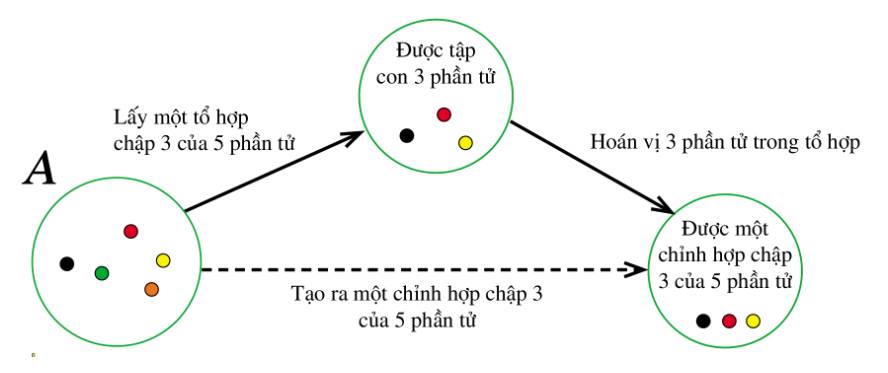
a) Cách lấy ra một tổ hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A ví dụ như \(\left\{ {a;b;c} \right\}\)
b) Cách lấy ra một chỉnh hợp chập 3 của 5 phần tử trong A là: Chọn bất kỳ 3 trong 5 phần tử thuộc A rồi sắp xếp theo một thứ tự nào ví dụ như ta chọn 3 phần tử a,b,c rồi sắp xếp theo thứ tự ngược của bảng chữ cái \(\left\{ {c;b;a} \right\}\)
c) So sánh: Mỗi tổ hợp chập 3 của 5 phần tử sinh ra 3! chỉnh hợp chập 3 của 5 phần tử vì có 3! hoán vị của 3 phần tử. Vì thế, số chỉnh hợp chập 3 của 5 phần tử nhiều gấp 3! lần số tổ hợp chập 3 của 5 phần tử.

Tập A có n phần tử:
Số tập con có 3 phân tử là: \(C_n^3=\frac{n!}{3!\left(n-3\right)!}=\frac{n\left(n-1\right)\left(n-2\right)}{6}\)
Số tập con 2 phần tử là : \(C_n^2=\frac{n!}{2!\left(n-2\right)!}=\frac{n\left(n-1\right)}{2}\)
Theo bài ra ta có: \(\frac{n\left(n-1\right)\left(n-2\right)}{6}-\frac{n\left(n-1\right)}{2}=14\)<=> \(n^3-6n^2+5n-84=0\Leftrightarrow n=7\)
Vậy tập A có 7 phần tử

Ta có: \(A=\left\{x\in N|\left(2x+6\right)\left(x-3\right)=0\right\}\)
Mà: \(x\in N^+\)
\(\Rightarrow\left(2x+6\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x+6=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=-6\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-3\left(ktm\right)\\x=3\left(tm\right)\end{matrix}\right.\)
Vậy tập hợp A là:
\(A=\left\{3\right\}\)
Số phần từ là 1
⇒ Chọn B