Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
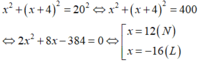
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Đáp án A
Gọi độ dài cạnh góc vuông nhỏ hơn của tam giác vuông đó là x (cm); (0 < x < 20)
Cạnh góc vuông lớn hơn của tam giác vuông có độ dài là: x + 4
Vì cạnh huyền bằng 20 cm nên theo định lý Py-ta-go ta có:
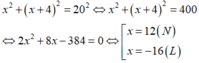
Vậy độ dài hai cạnh góc vuông của tam giác vuông đó lần lượt là: 12 cm và 12 + 4 = 16 cm

Gọi ba cạnh của ▲ là a,b,c>0
Giả sử cạnh huyền ▲ là a thì:
a² =b²+c² <=> b²+c²=13² =169 (1)
chu vi ▲ là 30 <=> a+b+c =30 <=> b+c = 30-13=17
<=> c= 17-b (2)
thay (2) vào (1) đc:
b² + (17-b)² =169 <=> b² -17b + 60 = 0
<=> (b-12)(b-5) = 0
<=> b=5 hoặc b=12
tương ứng c=12 và c=5
Vậy hai cạnh góc vuông dài 5m và 12m

Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có: x 2 + y 2 = 10 2 = 100 ( 2 )
Từ (1) và (2) ta có hệ phương trình:
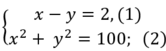
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
( y + 2 ) 2 + y 2 = 100 ⇔ y 2 + 4 y + 4 + y 2 = 100 ⇔ 2 y 2 + 4 y − 96 = 0 hay y 2 + 2 y − 48 = 0
Giải ra ta được: y 1 = 6 ; y 2 = - 8 < 0 ( loại)
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.

Gọi số đo độ dài hai cạnh góc vuông của tam giác vuông đó là x(cm), y (cm)
( 0 < y < x < 10)
Hai cạnh góc vuông có độ dài hơn kém nhau 2cm nên ta được x – y = 2 , (1).
Theo định lý Pytago ta có: x 2 + y 2 = 10 2 = 100 ( 2 )
Từ (1) và (2) ta có hệ phương trình:
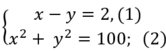
Từ (1) suy ra: x= y+ 2 thay vào (2) ta được:
( y + 2 ) 2 + y 2 = 100 ⇔ y 2 + 4 y + 4 + y 2 = 100
⇔ 2 y 2 + 4 y – 96 = 0 h a y y 2 + 2 y – 48 = 0
Giải ra ta được: y 1 = 6 ; y 2 = - 8 < 0 ( l o ạ i )
Với y= 6 suy ra x = 8.
Vậy độ dài các cạnh góc vuông của tam giác vuông là 6cm và 8cm.

gọi 2 canh tam giác là x và x+2
áp dụng định lí pytago ta có
x^2+(x+2)^2=10^2
suy ra x^2+x^2+4x+4=100
suy ra x=6 (vì x>0)
suy ra2 cạnh góc vuông là 6 và 8cm

Lời giải:
Gọi độ dài cạnh góc vuông lần lượt là $a$ và $b$ ($a>b>0$) (cm)
Áp dụng định lý Pitago: $a^2+b^2=60^2=3600(*)$
$a-b=12$
$\Leftrightarrow a=b+12$. Thay vào $(*)$ thì:
$(b+12)^2+b^2=3600$
$\Leftrightarrow 2b^2+24b-3456=0$
$\Leftrightarrow b^2+12b-1728=0$
$\Leftrightarrow (b-36)(b+48)=0$
Do $b>0$ nên $b=36$ (cm)
$a=b+12=36+12=48$ (cm)


Đáp án A