Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOKB vuông tại K và ΔOHC vuông tại H co
góc KOB=góc HOC
=>ΔOKB đồng dạng với ΔOHC
d: góc BKC=góc BHC=90 độ
=>BKHC nộitiếp
=>góc AKH=góc ACB
=>ΔAKH đồng dạng với ΔACB
=>\(\dfrac{S_{AKH}}{S_{ACB}}=\left(\dfrac{AK}{AC}\right)^2=\dfrac{1}{4}\)
=>\(S_{ABC}=32\left(cm^2\right)\)

a, Xét tam giác AHB và tam giác AKC ta có
^AHB = ^AKC = 900
^A _ chung
Vậy tam giác AHB ~ tam giác AKC ( g.g )
\(\Rightarrow\frac{AH}{AK}=\frac{AB}{AC}\Rightarrow\frac{AC}{AK}=\frac{AB}{AH}\)
b, Xét tam giác AHK và tam giác ABC ta có :
^A _ chung
\(\frac{AC}{AK}=\frac{AB}{AH}\)( cmt )
Vậy tam giác AHK ~ tam giác ABC ( c.g.c )
Do 2 tam giác đồng dạng theo trường hợp c.g.c tức là ^AHK = ^ABC
mà ^ABC = 580 => ^AHK = 580

b) Xét ΔBKC vuông tại K và ΔCHB vuông tại H có
\(\widehat{KBC}=\widehat{HCB}\)(ΔBAC cân tại A)
Do đó: ΔBKC\(\sim\)ΔCHB(g-g)
a) Áp dụng định lí Pytago vào ΔBKC vuông tại K, ta được:
\(BC^2=BK^2+CK^2\)
\(\Leftrightarrow CK^2=BC^2-BK^2=5^2-3^2=16\)
hay CK=4(cm)
Diện tích tam giác BKC là:
\(S_{BKC}=\dfrac{BK\cdot KC}{2}=\dfrac{3\cdot4}{2}=\dfrac{12}{2}=6\left(cm^2\right)\)

a: Xét ΔABC có AD là phân giác
nên DB/AB=DC/AC
=>DB/DC=AB/AC=2/3
=>3DB-2DC=0
mà DB+DC=18
nên DB=7,2cm; DC=10,8cm
b: Xét ΔBDH vuông tại H và ΔCDK vuông tại K có
góc BDH=góc CDK
=>ΔBDH đồng dạng với ΔCDK
=>BH/CK=BD/CD=2/3

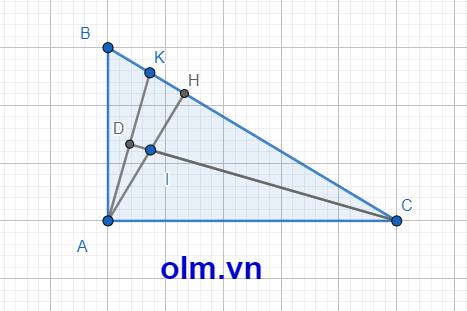
Xét \(\Delta\) HBA và \(\Delta\) ABC có \(\widehat{H}\) = \(\widehat{A}\) = 900; \(\widehat{B}\) chung
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) ABC (g-g)
Tương tự ta có: \(\Delta\) HAC \(\sim\) \(\Delta\) ABC (g-g-g)
⇒ \(\Delta\) HBA \(\sim\) \(\Delta\) HAC ( t/c hai tam giác đồng dạng)
⇒ \(\dfrac{HB}{HA}\) = \(\dfrac{HA}{HC}\) = \(\dfrac{BA}{AC}\)( theo khái niệm của tam giác đồng dạng.)
Mặt khác: KI là đường trung bình của tam giác ABH nên:
\(\dfrac{HI}{HA}\) = \(\dfrac{HK}{HB}\) ⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HB}{HA}\)
⇒ \(\dfrac{HK}{HI}\) = \(\dfrac{HA}{HC}\) mà \(\widehat{AHK}\) = \(\widehat{CHI}\) = 900
⇒ \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ( c-g-c)
b, Kéo dài CI cắt AK tại D ta có:
vì \(\Delta\) AHK \(\sim\) \(\Delta\) CHI ⇒ \(\widehat{HAK}\) = \(\widehat{HCI}\)
Xét \(\Delta\) HAK và \(\Delta\) DCK có: \(\widehat{A}\) = \(\widehat{C}\) ( cmt)
\(\widehat{K}\) chung
⇒ \(\Delta\) HAK \(\sim\) \(\Delta\) DCK ( g-g)
⇒ \(\widehat{H}\) = \(\widehat{D}\)= 900 ⇒ AK \(\perp\) CI tại D ( đpcm)