Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔHAB vuông tại H và ΔMAH vuông tại M có
góc HAB chung
Do đo:ΔHAB đồng dạng với ΔMAH
Xét ΔHAC vuông tại H và ΔNAH vuông tạiN có
góc HAC chung
Do đo: ΔHAC đồng dạng với ΔNAH
b: Xét ΔAHB vuông tại H có HMlàđường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔHAC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Ta có: \(AM\cdot AB=AN\cdot AC\)
nen AM/AC=AN/AB
Xét ΔAMN và ΔACB có
AM/AC=AN/AB
góc MAN chung
Do đó: ΔAMN\(\sim\)ΔACB

a) Xét \(\Delta HAB,\Delta MAH\) có :
\(\left\{{}\begin{matrix}\widehat{A}:Chung\\\widehat{AHB}=\widehat{AMH}=90^o\end{matrix}\right.\)
\(\Rightarrow\Delta HAB\sim\Delta MAH\left(g.g\right)\)
Xét \(\Delta HAC,\Delta NAH\) có :
\(\left\{{}\begin{matrix}\widehat{A}:chung\\\widehat{AHC}=\widehat{ANH}=90^o\end{matrix}\right.\)
=> \(\Delta HAC\sim\Delta NAH\left(g.g\right)\)
b) Từ \(\Delta HAB\sim\Delta MAH\left(g.g\right)\) ta có :
\(\dfrac{AM}{AH}=\dfrac{AH}{AB}\)
\(\Rightarrow AM.AB=AH^2\) (1)
Từ \(\Delta HAC\sim\Delta NAH\left(g.g\right)\) ta có :
\(\dfrac{AN}{AH}=\dfrac{AH}{AC}\)
\(\Rightarrow AN.AC=AH^2\) (2)
Từ (1) và (2) suy ra : \(AM.AB=AN.AC\left(=AH^2\right)\)
c) Xét \(\Delta AMN,\Delta ACB\) có :
\(\left\{{}\begin{matrix}AM.AB=AN.AC\left(cmt\right)\Leftrightarrow\dfrac{AM}{AN}=\dfrac{AC}{AB}\\\widehat{A}:Chung\end{matrix}\right.\)
\(\Rightarrow\Delta AMN\sim\Delta ACB\left(c.g.c\right)\)
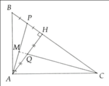
a: Xét ΔHAB vuông tại H và ΔMAH vuông tại M có
góc HAB chung
Do đó: ΔHAB\(\sim\)ΔMAH
Xét ΔHAC vuông tại H và ΔNAH vuông tại N có
góc HAC chung
Do đó: ΔHAC\(\sim\)ΔNAH
b: XétΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Xét ΔAMN và ΔACB có
AM/AC=AN/AB
góc MAN chung
Do đo: ΔAMN\(\sim\)ΔACB