Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BÀI TẬP 2:
Ta có:
\(\widehat{EOB}=\widehat{OBC}\left(EF//BC\right)\)
Mà \(\widehat{EBO}=\widehat{OBC}\left(g.t\right)\)
\(\Rightarrow\Delta BEO\text{ cân tại E.(đpcm)}\)
Tương tự:
\(\widehat{FOC}=\widehat{OCB}\left(EF//BC\right)\)
Mà \(\widehat{FCO}=\widehat{OCB}\left(g.t\right)\)
\(\Rightarrow\widehat{FOC}=\widehat{FCO}\)
\(\Rightarrow\Delta CFO\text{ cân tại }F.\left(đpcm\right)\)
b) Ta có:
\(\Delta BEO\text{ cân tại }E\)
\(\Rightarrow EB=EO\) (1)
Tương tự:
\(\Delta CFO\text{ cân tại }F\)
\(\Rightarrow OF=FC\left(2\right)\)
Mặt khác:
\(EF=EO=OF\left(3\right)\)
Từ (1), (2) và (3) \(\Rightarrow EF=EB+FC\left(đpcm\right)\)

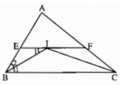
Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức là BI, CI lần lượt là tia phân giác của góc N và góc C. Do EF // BC nên ∠B1= ∠I1(so le trong), suy ra ∠I2 = ∠B2 .
Suy ra: BI, CI lần lượt là tia phân giác của góc B và góc C.
Do EF // BC nên ∠B1 = ∠BIE (so le trong).
Lại có: ∠B1 = ∠B2 ( vì BI là tia phân giác của góc B )
Suy ra: ∠B2 = ∠BIE
Vậy EF = EI + IF = BE + CF.

Vì điểm I cách đều ba cạnh của tam giác ABC và nằm trong tam giác nên I là giao điểm của ba đường phân giác của tam giác ABC, tức BI, CI lần lượt là tia phân giác của góc B và góc C. Do EF // BC nên \(\widehat{B_1}=\widehat{I_1}\) (hai góc so le trong), suy ra \(\widehat{I_1}=\widehat{B_2}\). Vậy tam giác EBI cân tại E, tức là EI = EB. Tương tự ta có FI = FC.
Vậy EF = EI + IF = BE + CF.

a. Xét Tam Giác ABC có góc A + góc B + góc C = 180 độ (định lí)
hay 90 độ + 50 độ + góc C = 180 độ
=> góc C = 180 độ - 90 độ - 50 độ
góc C = 40 độ
b. Xét tam giác ABC vuông tại A có :
BC2 = AC2 + AB2 (py-ta-go)
hay BC2 = 92 + 122
=> BC2 = 81+144
BC2 = 225
=> BC = 15cm
c. Xét tam giác vuông ABD và tam giác vuông EBD có
BD là cạnh chung
góc ABD = góc EBD (vì BD là tia phân giác góc ABC)
=> tam giác ABD = tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB ( 2 cạnh tương ứng )
d. Xét tam giác ABH và tam giác EBH có :
BH là cạnh chung
góc ABH = góc EBH (vì BD là tia phân giác góc ABC)
AB = EB (chứng minh trên)
=> tam giác ABH = tam giác EBH ( c.g.c )
=> góc BHA = góc BHE ( 2 góc tương ứng )
mà góc BHA + góc BHE = 180 độ ( 2 góc kề bù )
=> góc BHA = góc BHE = 90 độ
=> AE vuông góc với BH tại H
hay AE vuông góc với BD tại H.
Vì tam giác ABH = tam giác EBH ( chứng minh trên )
=> AH = EH ( 2 cạnh tương ứng )
=> H là trung điểm của AE.
câu e hơi khó, mình để sau :(
f. Vì tam giác ABD = tam giác EBD ( cmt)
=> AD = ED ( 2 cạnh tương ứng )
Xét tam giác ADF và tam giác EDC có :
góc FAD = góc DEC (= 90 độ )
AD = ED (cmt)
góc FDA = góc CDE ( 2 góc đối đỉnh )
=> tam giác ADF = tam giác EDC ( g.c.g)
=> AF = CE ( 2 cạnh tương ứng )
Vì AF = CE (cmt)
mà AB = EB (cmt)
=> AF + AB = CE + EB
hay BF = CB
=> tam giác BFC cân tại B
còn câu e, g, h mình bó tay, xin lỗi ;(
chúc bạn học tốt ![]()

Do AH\(\perp BC=\left\{H\right\}\) (gt)\(\Rightarrow\widehat{AHB}=90^0\)
\(A'H'\perp B'C'=\left\{H'\right\}\left(gt\right)\Rightarrow\widehat{A'H'B'}=90^0\)
Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
AH=A'H' (gt)
\(\widehat{AHB}=\widehat{A'H'B'}=90^0\left(cmt\right)\)
AB=BC=AC (gt)
\(\Rightarrow\Delta ABC=\Delta A'B'C'\left(c.g.c\right)\)
Chúc bn học tốt!