Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
AM là đường trung tuyến của tam giác ABC cân tại A
=> AM là đường cao của tam giác ABC cân tại A
=> AM _I_ BC
hay AMC = 900
I là trung điểm của AC (gt)
I là trung điểm của MN (M đối xứng N qua I)
=> AMCN là hình bình hành
mà AMC = 900
=> AMCN là hình chữ nhật
K là trung điểm của AB (gt)
M là trung điểm của BC (AM là đường trung tuyến của tam giác ABC)
=> KM là đường trung bình của tam giác ABC
=> KM = AC/2
mà IC = AC/2 (I là trung điểm của AC)
=> KM = IC
mà KM // IC (KM là đường trung bình của tam giác ABC)
=> MKIC là hình bình hành
b.
AN = MC (AMCN là hình chữ nhật)
mà MC = BM (M là trung điểm của BC)
=> AN = BM
mà AN // BM (AMCN là hình chữ nhật)
=> ANMB là hình bình hành
mà E là trung điển của AM
=> E là trung điểm của BN
c.
AMCN là hình vuông
<=> Tam giác ABC vuông cân tại A

a: Xét tứ giác MPNI có
Q là trung điểm chung của MN và PI
Do đó: MPNI là hình bình hành
b: Xét ΔNMP có NQ/NM=NK/NP
nên QK//MP
=>QK vuông góc với MN

A F E D B C M
Mình vẽ hình hơi xâu, bạn thông cảm nhé!
a) Xét từ giác ABMC có: + AM cắt BC tại D (bạn dùng ký hiệu giao nhé)
+ DA = DM (gt)
+ DB = DM(gt)
suy ra, tứ giác AMCM là hình bình hành mà ta có góc CAB là góc vuông suy ra tứ giác ABMC là hình chữ nhật
Các câu còn lại bạn đầu có thể giải theo cách trên nhé!
( e mk chưa làm đc, mk mới đc học đến bào hình chữ nhật thôi, sory)

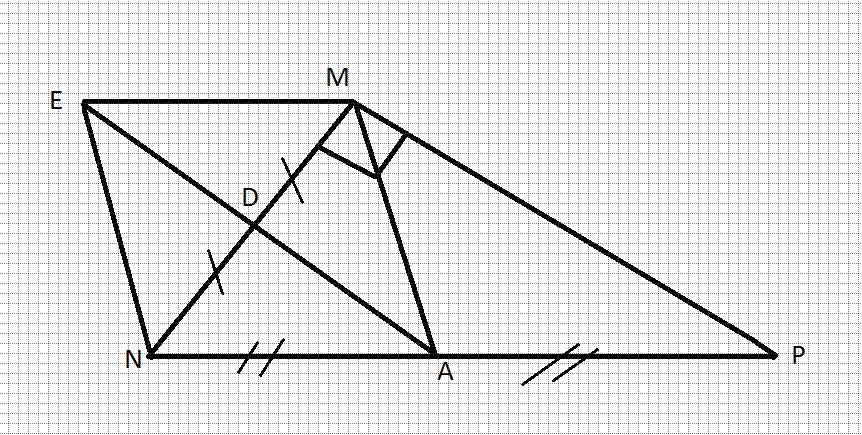
a: Xét ΔMNP có NA/NP=ND/NM
nên DA//MP
=>DA vuông góc với NM
=>EA vuông góc với NM
mà EA cắt NM tại trung điểm của EA
nên E đối xứng A qua MN
b: Xét tứ giác MENA có
D là trung điểm chung của MN và EA
AN=AM
Do đó: MENA là hình thoi
Xét tứ giác MNKP có
E là trung điểm của NP
E là trung điểm của MK
Do đó: MNKP là hình bình hành
mà \(\widehat{PMN}=90^0\)
nên MNKP là hình chữ nhật