Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác MKHQ có
\(\widehat{MKH}+\widehat{MQH}=180^0\)
Do đó: MKHQ là tứ giác nội tiếp
c: Xét tứ giác NQKP có
\(\widehat{NKP}=\widehat{NQP}=90^0\)
Do đó: NQKP là tứ giác nội tiếp

a: góc MIN=góc MHN=90 độ
=>MNHI nội tiếp
b: MNHI nội tiếp
=>góc NMH=góc NIH

a: góc NAP=góc NBP=90 độ
=>PA vuông góc MN và NB vuông góc MB
Xét ΔMNP có
NB,PA là đường cao
NB cắt PA tại H
=>H là trực tâm
=>MH vuông góc NP tại I
Xét ΔHAN vuông tại A và ΔHBP vuông tại B có
góc AHN=góc BHP
=>ΔHAN đồng dạng với ΔHBP
b: góc HIP+góc HBP=180 độ
=>HIPB nội tiếp
c: góc BAH=góc IMP
góc IAH=góc BNP
mà góc IMP=góc BNP
nên góc BAH=góc IAH
=>AH là phân giác của góc BAI
góc ABH=góc NMI
góc IBH=góc APN
mà góc NMI=góc APN
nên góc ABH=góc IBH
=>BH là phân giác của góc ABI

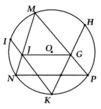
KG là đường phân giác của M K P ^ => M G G P = M K K P (1)
KJ là đường phân giác của M K N ^ => M J J N = M K K N (2)
Chứng minh được: KN = KP (3)
Từ (1); (2); (3) => M G G P = M J J N => Đpcm