
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



sử dụng phương pháp phát triển nâng cao dùng cho bồi dưỡng học sinh giỏi là gắn hệ tọa độ Oxy vào hình vẽ để làm

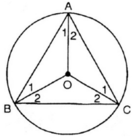
Vì tam giác ABC là tam giác đều nên 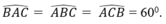
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
![]()
* Xét tam giác AOB có:
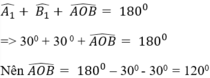
* Tượng tự ta được: ![]()
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)

a: Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
Suy ra: \(\widehat{OBA}=\widehat{OCA}\)
hay AC là tiếp tuyến của (O)
Đặt: \(AB=AC=BC=a\)
Độ dài a phải thoả mãn các bất đẳng thức trong tam giác:
\(\hept{\begin{cases}10-8< a< 10+8\\12-8< a< 12+8\\12-10< a< 12+10\end{cases}}\Leftrightarrow\hept{\begin{cases}2< a< 18\\4< a< 20\Leftrightarrow4< a< 18\left(\text{*}\right)\\2< a< 22\end{cases}}\)
\(\cos BAO=\frac{AO^2+AB^2-OB^2}{2.AO.AB}=\frac{a^2-36}{16a}\)
\(\cos CAO=\frac{AC^2+AO^2-OC^2}{2.AO.AB}=\frac{a^2-80}{16a}\)
Lại có:
\(\cos BAC=\cos\left(BAO+CAO\right)\)
\(\Leftrightarrow\cos60^o=\cos BAO.\cos CAO-\sin BAO.\sin CAO\)
\(\Leftrightarrow\frac{1}{2}=\cos BAO.\cos CAO-\sqrt{1-\cos^2BAO}.\sqrt{1-\cos^2CAO}\)
\(\Leftrightarrow\frac{1}{2}=\frac{a^2-36}{16a}.\frac{a^2-80}{16a}-\sqrt{1-\left(\frac{a^2-36}{16a}\right)^2}.\sqrt{1-\left(\frac{a^2-80}{16a}\right)^2}\)
\(\Leftrightarrow\frac{1}{2}=\frac{a^4-116a^2+2880}{256a^2}-\frac{\sqrt{\left(-a^4+328a^2-1296\right)\left(-a^4+416a^2-6400\right)}}{256a^2}\)
\(\Leftrightarrow128a^2=a^4-116a^2+2880-\sqrt{\left(-a^4+328a^2-1296\right)\left(-a^4+416a^2-6400\right)}\)
\(\Leftrightarrow\sqrt{\left(-a^4+328a^2-1296\right)\left(-a^4+416a^2-6400\right)}=a^4-244a^2+2880\) (1)
Điều kiện: \(a^4-244a^2+2880\ge0\left(\text{*}\text{*}\right)\)
\(\left(1\right)\Leftrightarrow a^8-744a^6+144144a^4-2638336a^2+8294400\)
\(=a^8+59536a^4+8294400-488a^6+5760a^4-1405440a^2\)
\(\Leftrightarrow256a^6-78848a^4+1232896a^2=0\)
\(\Leftrightarrow a^4-308a^2+4816=0\left(\Delta'=18900\Rightarrow\sqrt{\Delta'}=30\sqrt{21}\right)\)
\(\Leftrightarrow\orbr{\begin{cases}a^2=154+30\sqrt{21}\\a^2=154-30\sqrt{21}\end{cases}}\Rightarrow\orbr{\begin{cases}a=\sqrt{154+30\sqrt{21}}\left(\text{nhận}\right)\\a=\sqrt{154-30\sqrt{21}}\left(\text{loại vì không thoả }\left(\text{** }\right)\right)\end{cases}}\)
Vậy: \(AB=\sqrt{154+30\sqrt{21}}\)
Bổ sung cái thứ 2 thêm cái \(12-10< a< 12+10\) nữa , olm lưu thiếu hay mình viết thiếu k rõ nữa, tóm lại thêm cái đó vào nha ...