Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔEDC vuông tại D và ΔEHC vuông tại H có
EC chung
\(\widehat{DEC}=\widehat{HEC}\)
Do đó; ΔEDC=ΔEHC
b: Xét ΔDCK vuông tại D vàΔHCF vuông tại H có
CD=CH
\(\widehat{DCK}=\widehat{HCF}\)
Do đó; ΔDCK=ΔHCF
Suy ra: CK=CF
a, Xét Δ DCE và Δ HCE, có :
EC là cạnh chung
\(\widehat{CDE}=\widehat{CHE}=90^o\)
\(\widehat{DEC}=\widehat{HEC}\) (EC là tia phân giác \(\widehat{DEH}\))
=> Δ DCE = Δ HCE (g.c.g)
=> DC = HC
b, Xét Δ DCK và Δ HCF, có :
DC = HC (cmt)
\(\widehat{DCK}=\widehat{HCF}\) (đối đỉnh)
=> Δ DCK = Δ HCF ( ch - cgn)
=> CK = CF
=> Δ CKF cân tại C

b. Ta co goc EMD + goc EMH =90 mà DEM = HEM nen EMD = EMH. Xet 2 tam giac DEM va HEM có EH canh chung, goc EMH =EMD, DEM=HEM
C. EF=EK suy ra tam giac EFK can tai E. EM la tia phan giác, cung là đường cao, ta lại có ED vuong góc voi EK. Suy ra M là trực tâm. Mà MH vuong goc EF. Suy ra KMH thang hang

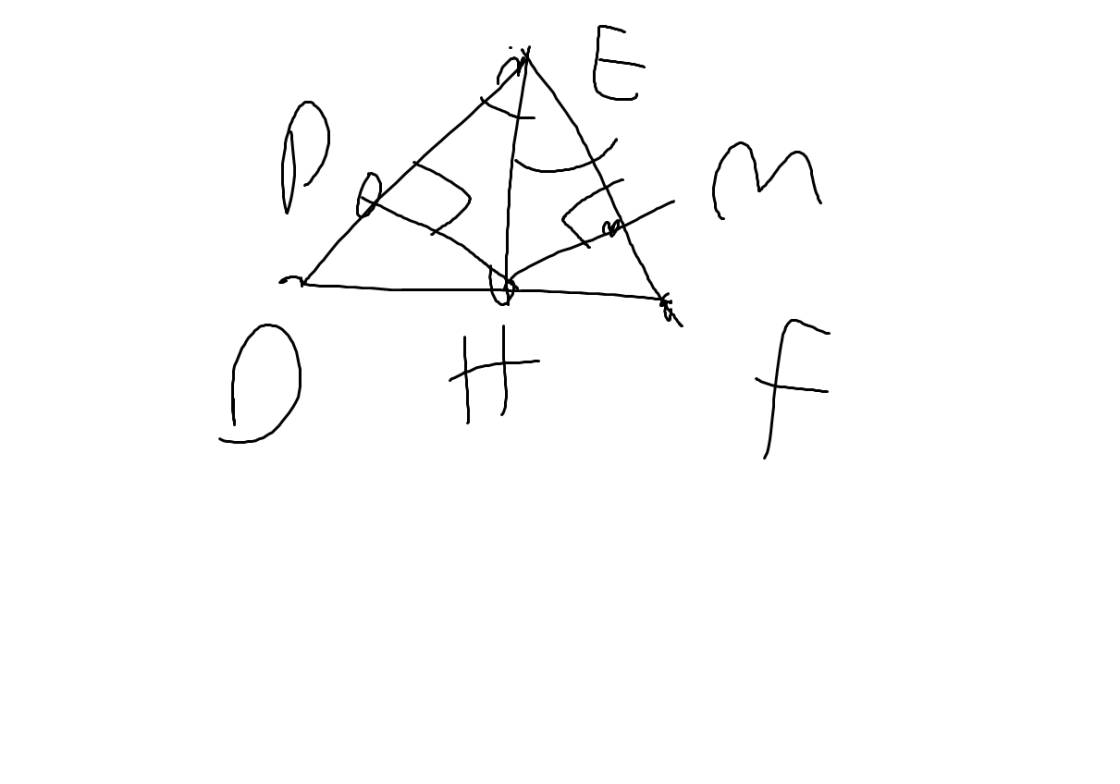
a: Xét ΔDEM vuông tại E và ΔDHM vuông tại H có
DM chung
góc EDM=góc HDM
=>ΔDEM=ΔDHM
b: Xét ΔMEK vuông tại E và ΔMHF vuông tại H có
ME=MH
góc EMK=góc HMF
=>ΔMEK=ΔMHF
=>MK=MF
=>ΔMKF cân tại M
c: KM+ME=EM+MF=EF<KF

a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)

a: Xét ΔEDA có ED=EA
nên ΔEDA cân tại E
b: Xét ΔDEB vuông tại D và ΔAEB vuông tại A có
BE chung
ED=EA
DO đó: ΔDEB=ΔAEB
Suy ra: DB=AB
a: Xét ΔEDC vuông tại D và ΔEHC vuông tại H có
EC chung
góc DEC=góc HEC
=>ΔEDC=ΔEHC
b: Xét ΔCDK vuông tại D và ΔCHF vuông tại H có
CD=CH
góc DCK=góc HCF
=>ΔCDK=ΔCHF
=>CK=CF
=>ΔCKF cân tại C