Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

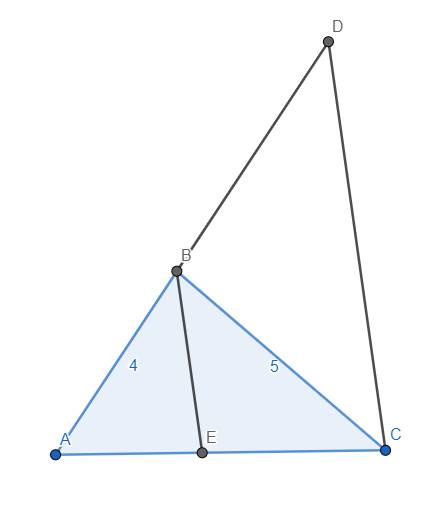
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.
b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)
Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\) nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\), suy ra \(AD=AB+BD=4+5=9\).
\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).
Vậy \(AC=6\)
Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.

Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{ABD}+60^0=180^0\)
hay \(\widehat{ABD}=120^0\)
\(\Leftrightarrow\widehat{DAB}=180^0-120^0-40^0=20^0\)
Xét ΔABD có
\(\dfrac{AB}{\sin40^0}=\dfrac{AD}{\sin120^0}=\dfrac{BD}{\sin20^0}\)
\(\Leftrightarrow\left\{{}\begin{matrix}AD\simeq6,74\left(cm\right)\\BD\simeq2,66\left(cm\right)\end{matrix}\right.\)

a) Ta có: \(\widehat{ABD}+\widehat{ABC}=180^0\)(hai góc kề bù)
nên \(\widehat{ABD}=120^0\)
Xét ΔABD có
\(\widehat{ABD}+\widehat{BAD}+\widehat{ADB}=180^0\)(Định lí tổng ba góc trong một tam giác)
hay \(\widehat{BAD}=20^0\)
Xét ΔABD có
\(\dfrac{AB}{\sin\widehat{D}}=\dfrac{DB}{\sin\widehat{BAD}}=\dfrac{AD}{\sin\widehat{ABD}}\)
\(\Leftrightarrow\dfrac{DB}{\sin20^0}=\dfrac{AD}{\sin120^0}=\dfrac{5}{\sin40^0}\)
Suy ra: \(\left\{{}\begin{matrix}DB\simeq2,66\left(cm\right)\\AD\simeq6,74\left(cm\right)\end{matrix}\right.\)

\(a,\) Kẻ đường cao AH
Suy ra AH là đường cao cũng là trung tuyến
Do đó \(BH=HC=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng PTG: \(AH=\sqrt{AB^2-BH^2}=\sqrt{a^2-\dfrac{a^2}{4}}=\dfrac{a\sqrt{3}}{2}\)
Vậy \(S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot\dfrac{a\sqrt{3}}{2}\cdot a=\dfrac{a^2\sqrt{3}}{4}\left(đvdt\right)\)

làm bừa thui,ai tích mình mình tích lại
Số số hạng là :
Có số cặp là :
50 : 2 = 25 ( cặp )
Mỗi cặp có giá trị là :
99 - 97 = 2
Tổng dãy trên là :
25 x 2 = 50
Đáp số : 50

