Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: AD=ED
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
c: Ta có: ΔADF=ΔEDC
nên DF=DC và AF=EC
Ta có: BA+AF=BF
BE+EC=BC
mà BA=BE
và AF=EC
nên BC=BF
hay B nằm trên đường trung trực của CF(1)
Ta có: DF=DC
nên D nằm trên đường trung trực của CF(2)
Từ (1) và (2) suy ra BD\(\perp\)CF

Lười đánh máy thật sự:vvv
a) Xét ∆ABD và ∆AED:
AD: cạnh chung
AB=AE(gt)
\(\widehat{BAD}=\widehat{CAD}\) (AD là phân giác góc BAC)
=> ∆ABD=∆AED (c.g.c)
=> BD=DC
b) Theo câu a: ∆ABD=∆AED
=> \(\widehat{ABD}=\widehat{AED}\)
Ta có: \(\left\{{}\begin{matrix}\widehat{ABD}+\widehat{DBK}=180^o\\\widehat{AED}+\widehat{DEC}=180^o\end{matrix}\right.\)
\(\Rightarrow\widehat{DBK}=\widehat{DEC}\)
Xét ∆DBK và ∆DEC:
BD=ED(cm ở a)
\(\widehat{DBK}=\widehat{DEC}\left(cmt\right)\)
\(\widehat{BDK}=\widehat{EDC}\) ( 2 góc đối đỉnh)
=> ∆DBK=∆DEC (g.c.g)
c) Gọi giao điểm của AD và BE là I
Xét ∆BAI và ∆EAI:
AB=AE(gt)
\(\widehat{BAI}=\widehat{EAI}\left(gt\right)\)
AI: cạnh chung
=> ∆BAI=∆EAI (c.g.c)
=> \(\left\{{}\begin{matrix}BI=EI\left(1\right)\\\widehat{AIB}=\widehat{AIE}\end{matrix}\right.\)
Mà \(\widehat{AIB}+\widehat{AIE}=180^o\) (2 góc kề bù)
=> \(\widehat{AIB}=\widehat{AIE}=90^o\left(2\right)\)
Từ (1) và (2) suy ra AD là trung trực của BE.
a) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
AE chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)

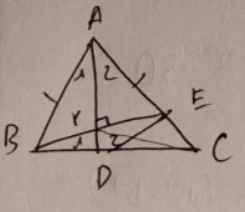
a Xét tam giác ABD và tam giác AED có:
\(\widehat{A_1}=\widehat{A_2}\)
AB = AE
BD chung
=> ΔABD = ΔAED (c.g.c)
=> BD = DE
b Xét △DBK và △DEC có:
DB = DE (cmt)
KD chung
\(\widehat{D_1}=\widehat{D_2}\)
=> △DBK=△DEC (c.g.c)

a: Xét ΔADB và ΔADE có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔADB=ΔADE
Suy ra: BD=ED
b: Ta có: ΔADB=ΔADE
nên \(\widehat{ABD}=\widehat{AED}\)
hay \(\widehat{DBK}=\widehat{DEC}\)
Xét ΔDBK và ΔDEC có
\(\widehat{DBK}=\widehat{DEC}\)
DB=DE
\(\widehat{BDK}=\widehat{EDC}\)
Do đó: ΔDBK=ΔDEC
c: Ta có: AB+BK=AK
AE+EC=AC
mà AB=AE
và BK=EC
nên AK=AC
Xét ΔAKC có AK=AC
nên ΔAKC cân tại A
d: Ta có: ΔDBK=ΔDEC
nên DK=DC
Ta có: AK=AC
nên A nằm trên đường trung trực của CK(1)
Ta có: DK=DC
nên D nằm trên đường trung trực của CK(2)
Từ (1) và (2) suy ra AD là đường trung trực của CK
hay AD\(\perp\)CK

a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED

1) Xét ΔABD và ΔAED có
AB=AE(gt)
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAD}\))
AD chung
Do đó: ΔABD=ΔAED(c-g-c)
Suy ra: BD=ED(hai cạnh tương ứng)
2) Ta có: ΔABD=ΔAED(cmt)
nên \(\widehat{ABD}=\widehat{AED}\)(hai góc tương ứng)
Ta có: \(\widehat{ABD}+\widehat{KBD}=180^0\)(hai góc kề bù)
\(\widehat{AED}+\widehat{CED}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AED}\)(cmt)
nên \(\widehat{KBD}=\widehat{CED}\)
Xét ΔDBK và ΔDEC có
\(\widehat{KBD}=\widehat{CED}\)(cmt)
BD=ED(cmt)
\(\widehat{BDK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDBK=ΔDEC(g-c-g)
3) Ta có: ΔDBK=ΔDEC(cmt)
nên BK=EC(hai cạnh tương ứng)
Ta có: AB+BK=AK(B nằm giữa A và K)
AE+EC=AC(E nằm giữa A và C)
mà AB=AE(gt)
và BK=EC(cmt)
nên AK=AC
Xét ΔAKC có AK=AC(cmt)
nên ΔAKC cân tại A(Định nghĩa tam giác cân)