Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

, Tự vẽ hình và ghi giả thiết kết luận (mình không biết vẽ hình trên máy -_-")
Giải : Từ giả thiết ta có
D là trung điểm của AB và MO
,E là trung điểm của AC và ON
=> ED là đường trung bình của cả hai tam giác ABC và OMN
Áp dụng định lý đường trung bình vào tam giác trên ,ta được
\(\hept{\begin{cases}AD//BC,DE//MN\\DE=\frac{1}{2}BC,DE=\frac{1}{2}MN\end{cases}}\Rightarrow\hept{\begin{cases}MN//BC\\MN=BC\end{cases}}\)
Tứ giác MNCB có hai cạnh đối song song và bằng nhau nên nó là hình bình hành
Từ từ ,hình như mình làm nhầm đề :) Để mình làm lại đã rồi trả lời bn sau nhé!!!!!@@

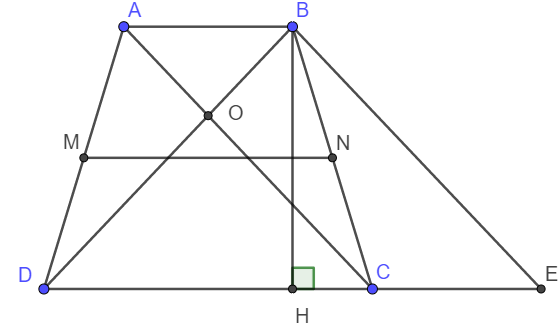
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.

Bài 1 :
a) Ta có : \(\hept{\begin{cases}AM=MB\\AN=NC\end{cases}\Rightarrow}\)MN là đường trung bình tam giác ABC \(\Rightarrow MN\text{//}BC\) hay \(MN\text{//}HK\left(1\right)\)
Dễ thấy MNKB là hình bình hành => \(\widehat{MNK}=\widehat{ABC}=\widehat{MHB}\)(Vì tam giác AHB vuông có HM là đường trung tuyến ứng với cạnh huyền.) . Mặt khác : \(\widehat{MNK}=\widehat{CKN}\)(hai góc ở vị trí so le trong)
=> \(\widehat{MHB}=\widehat{CKN}\). Mà hai góc này lần lượt bù với \(\widehat{MHK}\)và \(\widehat{HKN}\)=> \(\widehat{MHK}=\widehat{HKN}\) (2)
Từ (1) và (2) suy ra MNKH là hình thang cân.
b) Dễ thấy HK là đường trung bình tam giác AED => HK // ED hay BC // ED (3)
Tương tự , MH và NK lần lượt là các đường trung bình của các tam giác ABE và ACD
=> BE = 2MH ; CD = 2NK mà MH = NK (MNKH là hình thang cân - câu a)
=> BE = CD (4)
Từ (3) và (4) suy ra BCDE là hình thang cân.
Bài 2 :
a) Ta có : \(\widehat{BAD}=\widehat{CAE}=90^o\Rightarrow\widehat{BAD}+\widehat{DAE}=\widehat{CAE}+\widehat{DAE}\Rightarrow\widehat{BAE}=\widehat{CAD}\)
Xét tam giác BAE và tam giác CAD có : \(AB=AD\left(gt\right)\); \(AC=AE\left(gt\right)\) ; \(\widehat{BAE}=\widehat{CAD}\left(cmt\right)\)
\(\Rightarrow\Delta BAE=\Delta CAD\left(c.g.c\right)\Rightarrow CD=BE\)
b) Dễ dàng chứng minh được MP và PN lần lượt là các đường trung bình của các tam giác ACD và tam giác BEC
=> MP = 1/2CD ; PN = 1/2 BE mà CD = BE => MP = PN => tam giác MNP cân tại P
Để chứng minh góc MPN = 90 độ , hãy chứng minh BE vuông góc với CD.
DƯƠNG PHAN KHÁNH DƯƠNG :