Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔANB vuông tại N và ΔANC vuông tại N có
AN chung
NB=NC
Do đó: ΔANB=ΔANC
b: Xét ΔNAB vuông tại N và ΔNMC vuông tại N có
NA=NM
NB=NC
Do đó: ΔNAB=ΔNMC
=>\(\widehat{NAB}=\widehat{NMC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//MC
c: N là trung điểm của BC
=>BC=2*BN=12(cm)
Chu vi tam giác ABC là:
\(C_{ABC}=AB+AC+BC\)
=10+10+12
=32(cm)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
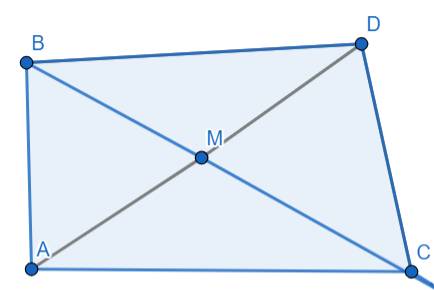
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC và AB=EC
c: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔBCD cân tại C
d: Xét ΔOBC có
OM là đường cao
OM là đường trung tuyến
Do đó: ΔOBC cân tại O
Suy ra: OB=OC(1)
Xét ΔOBD có
OA là đường cao
OA là đường trung tuyến
Do đó: ΔOBD cân tại O
Suy ra: OB=OD(2)
Từ (1) và (2) suy ra OB=OC=OD
hay O cách đều ba đỉnh của ΔBDC

a) \(\Delta ABC\) vuông tại A áp dụng định lý Py-ta-go ta có:
\(BC=\sqrt{AC^2+AB^2}=\sqrt{15^2-8^2}=17\left(cm\right)\)
b) Xét \(\Delta ABM\) và \(\Delta DMC\) ta có:
\(MA=MD\left(gt\right)\)
\(\widehat{BMA}=\widehat{DMC}\) (hai góc đổi đỉnh)
\(BM=MC\) (M là trung điểm của BC)
\(\Rightarrow\Delta ABM=\Delta DMC\left(c-g-c\right)\)

Hình tự vẽ nha !
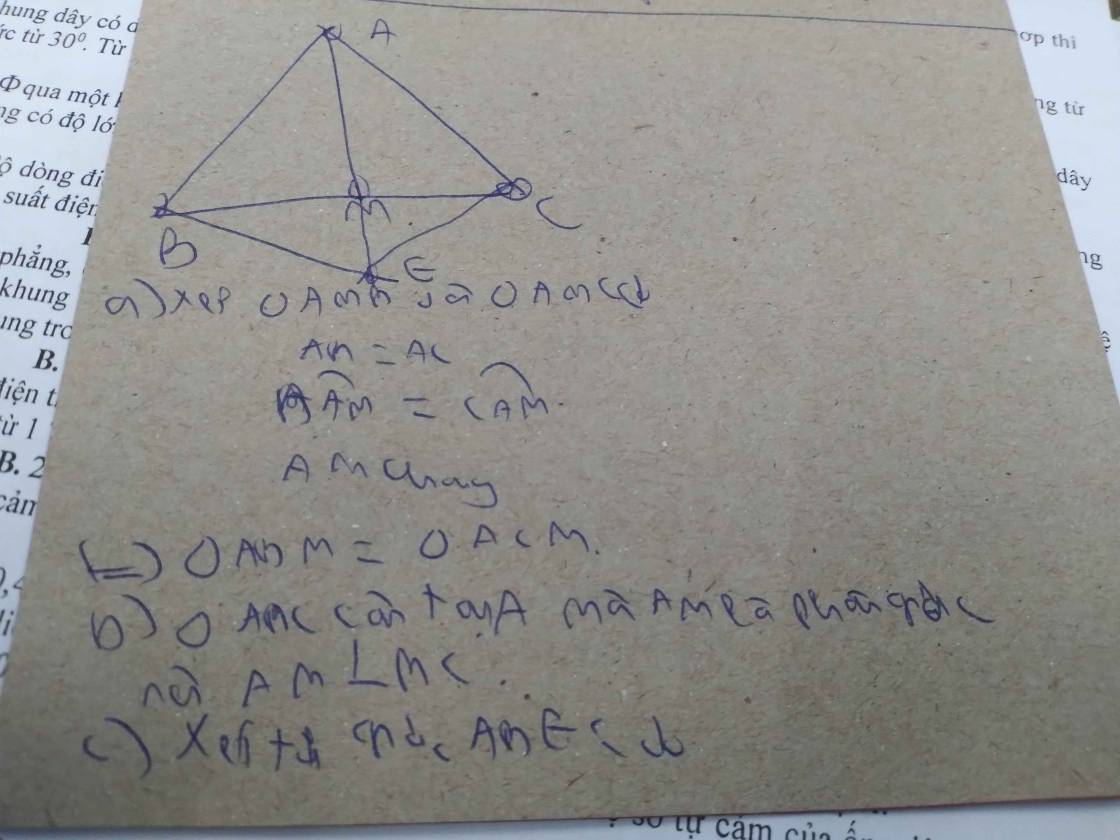
a/ Xét ΔABM và ΔECM có:
MB=MC (Mlà trung điểm của BC)
góc AMB = góc EMC ( 2 góc đối đỉnh)
MA=ME(giả thiết)
Do đó ΔABM=ΔECM(c.g.c)
b/ vì ΔABM=ΔECM nên góc BAM= góc MEC (2 góc tương ứng)
mà góc BAM và góc MEC là 2 góc ở vị trí so le trong ( khi đoạn thẳng AE cắt AB và CE ở A và E) nên theo dấu hiệu nhận biết 2 đường thẳng song song => AB // CE
c/ mik ko bt

a: Xét ΔANB và ΔAMC có
AN=AM
góc A chung
AB=AC
Do đó: ΔANB=ΔAMC
b: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
c: góc ABI+góc IBC=góc ABC
góc ACI+góc ICB=góc ACB
mà góc ABI=góc ACI;góc ABC=góc ACB
nên góc IBC=góc ICB
=>ΔIBC cân tại I
=>I nằm trên trung trực của BC
mà AD là trung trực của BC
nên A,I,D thẳng hàng

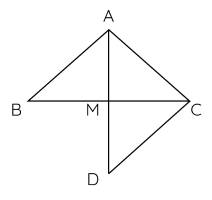
a) Xét hai tam giác $AMB$ và $AMC$ có:
$AM$ là cạnh chung;
$AB = AC$ (gt);
$BM = MC$ ($M$ là trung điểm $BC$);
Suy ra $\Delta AMB=\Delta AMC$ (c.c.c)
b) $\Delta AMB=\Delta AMC$ suy ra
$\widehat{BAM} = \widehat{CAM}$ (hai góc tương ứng)
Suy ra $AM$ là tia phân giác của góc $BAC$.
c) Xét hai tam giác $AMD$ và $DMC$ có:
$AM = AD$ (gt);
$\widehat{AMB} = \widehat{CMD}$ (hai góc đối đỉnh);
$BM = MC$.
Nên $\Delta AMD=\Delta DMC$ (c.g.c)
Suy ra $\widehat{BAM} = \widehat{CDM}$ (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong nên $AB$ // $CD$.

a/ Trong TG ABC : AB2=BC2-AC2 (đ/l Pytago đảo)
AB2=102-82=62
=> TG ABC là TG vuông .


bạn ơi,bạn có viết sai đề ko.SAO có N là trung điểm mà trên tia đối MA là sao