
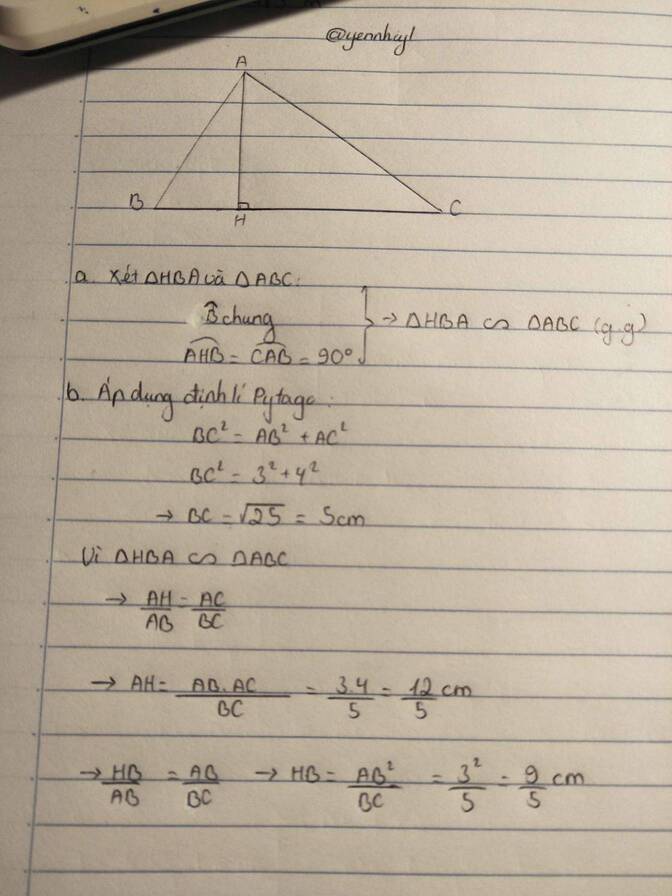
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

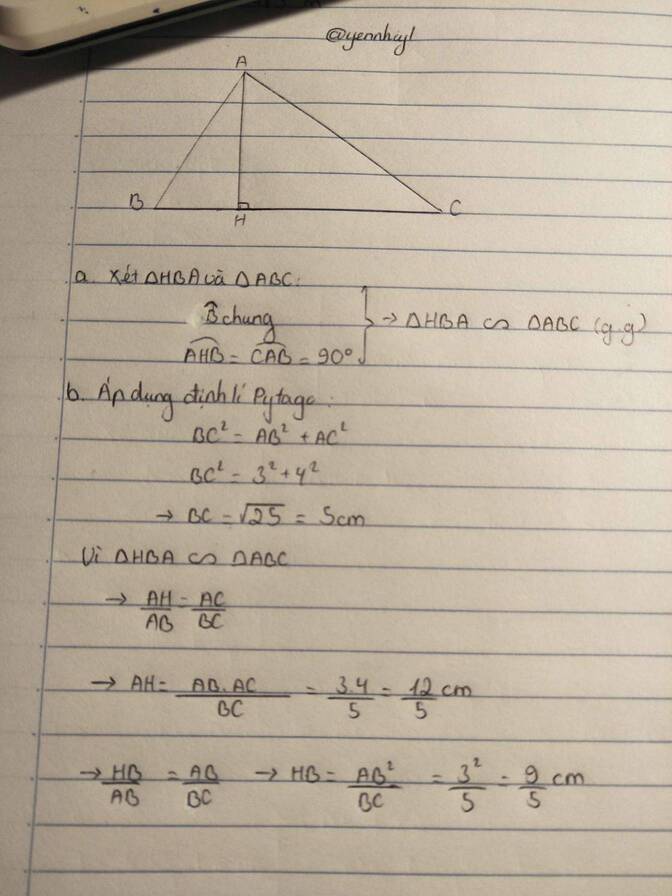

a)
Xét \(\Delta ABC\) và \(\Delta HBA\)có:
\(\widehat{BAC}=\widehat{AHB}\left(=90^ô\right)\)
\(\widehat{ABC}\)là góc chung (giả thiết)
Suy ra \(\Delta ABC\)đồng dạng với \(\Delta HBA\)(g.g)
b)
\(\Delta ABC\)vuông tại A
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(\Delta ABC\)đồng dạng với \(\Delta HBA\)
\(\Rightarrow\frac{AC}{AH}=\frac{BC}{AB}\Leftrightarrow AH=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4\left(cm\right)\)
c) Ta có
\(\hept{\begin{cases}\text{AH//DE}\\\widehat{AHC}=90^o\end{cases}\Rightarrow\widehat{CDE}=90^o}\)
Xét \(\Delta ABC\)và \(\Delta DEC\)có
\(\widehat{BAC}=\widehat{CDE}=90^o\)
\(\widehat{ACB}\)là góc chung (giả thiết)
Suy ra \(\Delta ABC\)đồng dạng với \(\Delta DEC\)(g.g)
\(\Rightarrow\frac{CA}{CB}=\frac{CD}{CE}\Leftrightarrow CE.CA=CD.CB\left(đpcm\right)\)
d)
\(\Delta AHB\)vuông tại H
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{3^2-2,4^2}=1,8\left(cm\right)\)
Ta có; \(CD=BC-BH-DH=5-1,8-2,4=0,8\left(cm\right)\)
Ta lại có:
\(\frac{CA}{CB}=\frac{CD}{CE}\)(theo câu c)
\(\Rightarrow EC=\frac{CB.CD}{CA}=\frac{5.0,8}{4}=1\left(cm\right)\)
Ta lại có:
\(AE=AC-EC=4-1=3\left(cm\right)\)
mà \(AB=3cm\)nên \(AB=AE\)hay \(\Delta ABE\)cân tại A
Vậy \(\Delta ABE\)cân tại A

a.Xét tam giác HBA và tam giác ABC, có:
^AHB = ^CAB = 90 độ
^B: chung
Vậy tam giác HBA đồng dạng tam giác ABC ( g.g )
b.
Áp dụng định lý pitago, ta có:
\(BC=\sqrt{8^2+10^2}=2\sqrt{41}cm\)
Ta có: tam giác HBA đồng dạng tam giác ABC
\(\Rightarrow\dfrac{AH}{AC}=\dfrac{AB}{BC}\)
\(\Leftrightarrow\dfrac{AH}{10}=\dfrac{8}{2\sqrt{41}}\)
\(\Leftrightarrow AH=\dfrac{8.10}{2\sqrt{41}}=\dfrac{40\sqrt{41}}{41}cm\)
Ta có: tam giác HBA đồng dạng tam giác ABC
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{AB}{BC}\)
\(\Leftrightarrow AB^2=HB.BC\)
\(\Leftrightarrow8^2=2\sqrt{41}HB\)
\(\Leftrightarrow HB=\dfrac{32\sqrt{41}}{41}cm\)

a, Xét tam giác HBA và tam giác ABC có
^B _ chung ; ^BHA = ^BAC = 900
Vậy tam giác HBA ~ tam giác ABC (g.g)
b, Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=10cm\)
\(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{48}{10}=\dfrac{24}{5}cm\)
\(\dfrac{BH}{AB}=\dfrac{AB}{BC}\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{36}{10}=\dfrac{18}{5}cm\)

a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5(cm)
Ta có: ΔHBA\(\sim\)ΔABC(cmt)
nên \(\dfrac{BH}{BA}=\dfrac{BA}{BC}=\dfrac{AH}{CA}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{BH}{3}=\dfrac{3}{5}=\dfrac{AH}{4}\)
Suy ra: BH=1,8cm; AH=2,4cm

a) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{B}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)

a)Ta có:`AB^2+AC^2=21^2+28^2=1225`
Mà `BC^2=1225`
Áp udnjg định lý ppytago đảo vào tam giác ABC có:`AB^2+AC^2=BC^2=1225`
`=>` tam giác ABC vuông
b)Vì BAC vuông tại A
`=>hat{BAC}=90^o`
`=>hat{HAB}=hat{HCA}=90^o-hat{HAC}`
Xét tam giác HBA và tam giác HAC có"
`hat{HAB}=hat{HCA}`(CMT)
`hat{BHA}=hat{HAC}=90^o`
`=>` tam giác HBA đồng dạng với tam giác HAC(gg)
c)Xét tam giác ACH và tam giác BAC ta có:
`hat{AHC}=hat{BAC}=90^o`
`hat{ACB}` chung
`=>DeltaACH~DeltaBAC(gg)`
`=>(AC)/(BH)=(BC)/(AC)`
`=>AC^2=BH.BC`.
d)Đường phân góc gì nhỉ?

a: Xet ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AH=6*8/10=4,8cm
BH=6^2/10=3,6cm

a: BC=căn 6^2+8^2=10cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
c: HB=AB^2/BC=6^2/10=3,6cm
HC=10-3,6=6,4cm