Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Bạn tự vẽ hình)
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền = 1/2 cạnh huyền
=> đpcm

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC

a) Xét ΔABE và ΔCKE có
EB=EK(gt)
\(\widehat{AEB}=\widehat{CEK}\)(hai góc đối đỉnh)
EA=EC(E là trung điểm của AC)
Do đó: ΔABE=ΔCKE(c-g-c)
b) Xét ΔAME vuông tại M và ΔCNE vuông tại N có
EA=EC(E là trung điểm của AC)
\(\widehat{AEM}=\widehat{CEN}\)(hai góc đối đỉnh)
Do đó: ΔAME=ΔCNE(Cạnh huyền-góc nhọn)
Suy ra: AM=CN(hai cạnh tương ứng)

a) Xét ΔABM và ΔDCM có:
BM=MC(gt)
\(\widehat{BMA}=\widehat{CMD}\)(đđ)
AM=DM
=> ΔABM=ΔDCM(c.g.c)
=>\(\widehat{ABM}=\widehat{MCD}\) .Mà 2 góc này ở vị trí soletrong)
=>AB//CD
b)Vì ΔABC vuông tại A(gt)
=> AM=BM=MC
Có: AD=AM+MD
BC=MB+MC
Mà: AM=BM(cmt); MD=MC(cmt)
=>BC=AM
Vì ΔABM=ΔDCM(cmt)
=>AB=DC
Xét ΔABC và ΔCDA có:
AB=DC(cmt)
AC: cạnh chung
BC=AD(cmt)
=>ΔABC=ΔCDM(c.c.c)
c) Vì ΔABC vuông tại A(gt)
=>AM=BC/2

Từ M kẻ \(MH\perp AC\) (H thuộc AC) ta có
\(MH\perp AC\)
\(AB\perp AC\)
=> MH//AB (cùng vuông góc với AC) (1)
BM=CM (2)
=> AH=CH (trong tam giác đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)
Trong ta giác AMC có
\(MH\perp AC;AH=HC\) => tam giác AMC cân tại M (ta giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
=> AM=CM mà CM=BM => AM=BM=CM \(\Rightarrow AM=\frac{1}{2}BC\)

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC


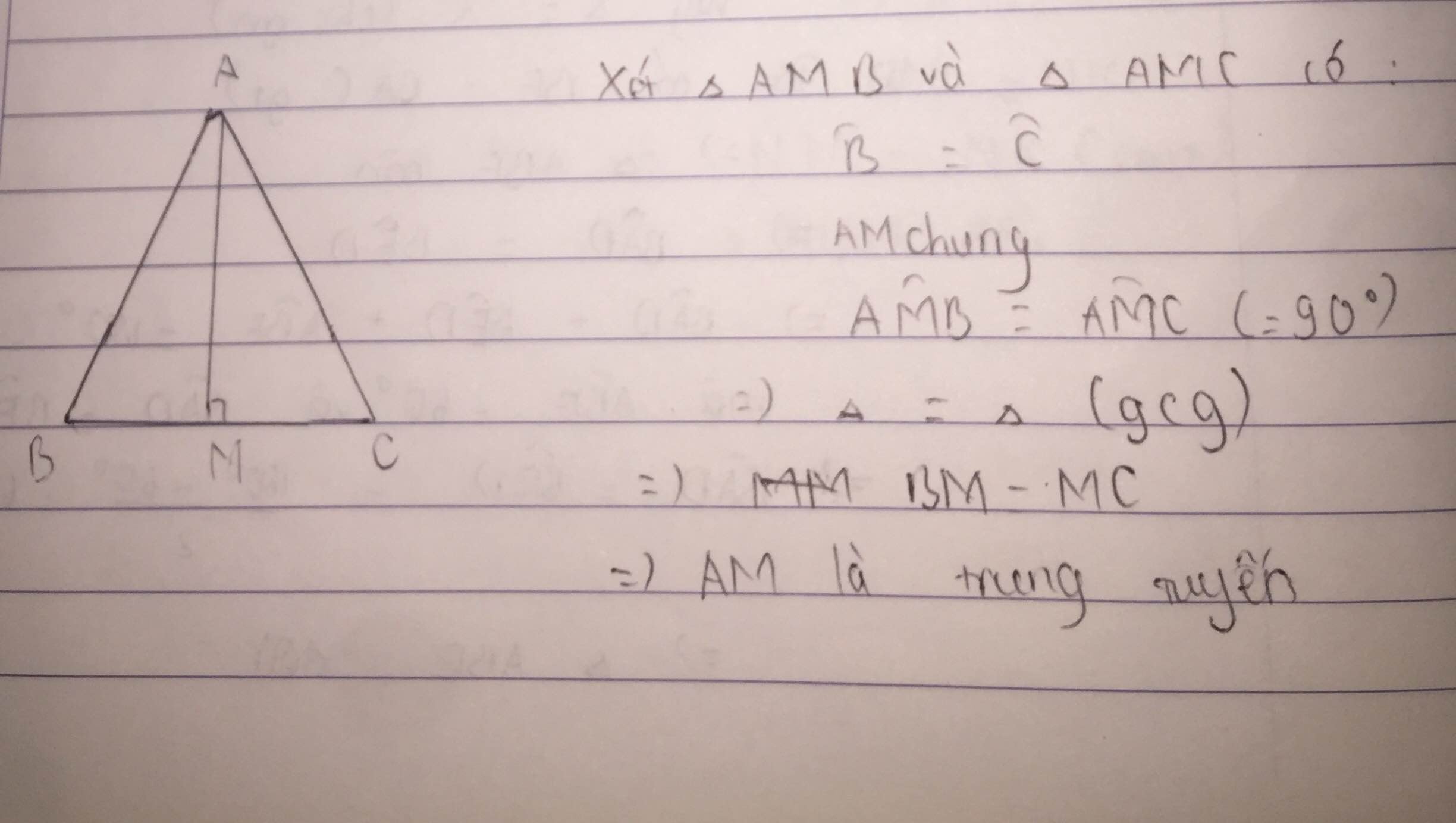
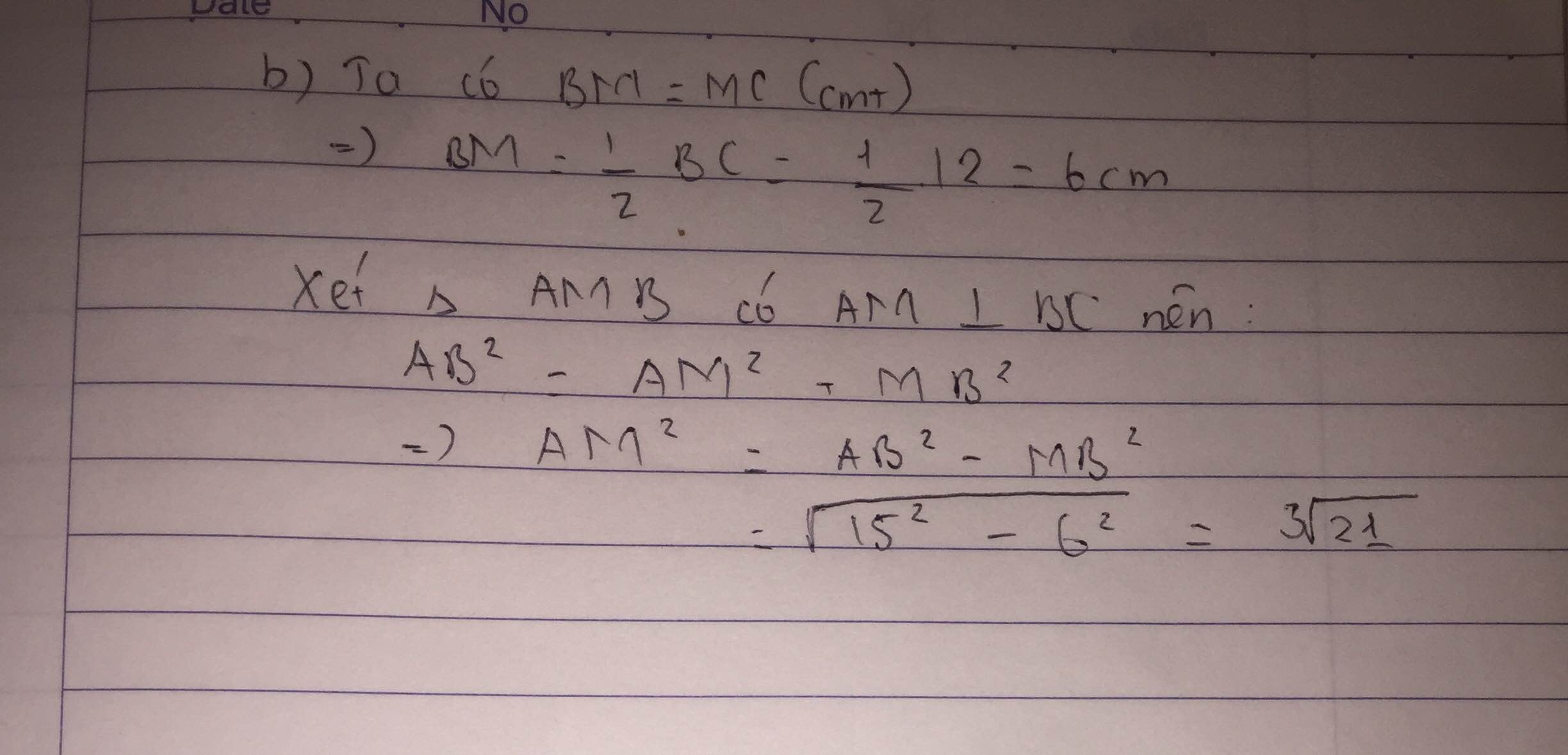
Trên tia đối của tia MA lấy D s/c MA=MD từ đó chứng minh được:
\(\text{△AMB=△DMC(c.g.c)}\) \(\text{⇒}\) \(\widehat{ABM}=\widehat{DCM}\) \(mà\) \(\widehat{ABM}+\widehat{ACM}=90^O\text{ }\text{⇒}\widehat{ACD}=90^O\)
⇒ \(\text{△}ABC=\text{△}CDA\left(c.g.c\right)\) ⇒ BC=AD ⇒ \(\dfrac{1}{2}BC=\dfrac{1}{2}AD\text{⇒ }\dfrac{1}{2}BC=AM\)
vì AM là trung tuyến TG ABC => M là trung điểm BC