Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Nối AM
Do BA = BM => △ABM cân tại A
=> BAM = BMA
Ta có: BAM + MAN = 90o => BMA + MAN = 90o
Lại có: MAN + AMN = 90o (△MAN vuông tại N)
=> HMA = NMA
Xét △HMA và △NMA có:
MHA = MNA (= 90o)
AM: chung
HMA = NMA (cmt)
=> △HMA = △NMA (ch-gn)
=> AH = AN (2 cạnh tương ứng)
=> △AHN cân tại A
b) Xét △ABC vuông tại A
=> BC2 = AB2 + AC2 (định lí Pytago)
=> AB2 + AC2 + AH > AB2 + AC2
=> BC + AH > AB + AC
c) Câu này hình như phải là chứng minh 2AC2 - BC2 = CH2 - BH2 chứ nhỉ? Nếu vậy thì cách làm như sau:
Xét △HAC vuông tại H
=> AC2 = HC2 + HA2 (định lí Pytago)
=> HC2 = AC2 - HA2
Xét △BHA vuông tại H
=> AB2 = HB2 + HA2 (định lí Pytago)
=> HB2 = AB2 - HA2
Khi đó:
CH2 - BH2 = AC2 - HA2 - AB2 + HA2
=> CH2 - BH2 = AC2 - AB2
=> CH2 - BH2 = AC2 + AC2 - BC2 (đpcm)

Xet ΔABC vuông tại A và ΔADE vuông tại A có
AB=AD
AC=AE
=>ΔABC=ΔADE
=>BC=DE

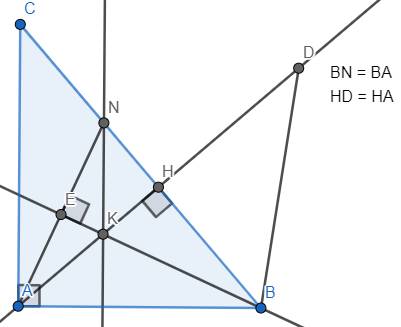
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)

https://h.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+vu%C3%B4ng+t%E1%BA%A1i+A.%28AB%3CAC%29+%C4%91%C6%B0%E1%BB%9Dng+cao+AH.+Tr%C3%AAn+c%E1%BA%A1nh+BC+l%E1%BA%A5y+M+sao+cho+BM%3DBA.+T%E1%BB%AB+M+k%E1%BA%BB+%C4%91%C6%B0%E1%BB%9Dng+th%E1%BA%B3ng+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+AC%28N+thu%E1%BB%99c+AC%29+c%2Fm%3A++a%29+tam+gi%C3%A1c+AHN+c%C3%A2n++b%29+BC%2BAH%3EAB%2BAC++c%29+2AC2-BC%3DCH2-BH2&subject=0
k bt giải nhờ mạng |~ mạng giải ~ thông cảm cho