Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ta có: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét ΔCAB có
H,K lần lượt là trung điểm của CB,CA
=>HK là đường trung bình của ΔCAB
=>HK//AB và \(HK=\dfrac{AB}{2}\)
Xét tứ giác AKHB có KH//AB
nên AKHB là hình thang
b: Ta có: AD\(\perp\)AH
BC\(\perp\)AH
Do đó: AD/BC
=>AD//BH
Xét tứ giác ADHB có
AD//HB
AB//HD
Do đó: ADHB là hình bình hành

a: Xét tứ giác AEID có
góc AEI=góc ADI=góc DAE=90 độ
nên AEID là hình chữ nhật
b: Xét ΔBAC co DI//AC
nên DI/AC=BI/BC=BD/BA=1/2
=>D là trung điểm của AB
Xét ΔBAC có EI//AB
nên EI/AB=CI/CB=CE/CA=1/2
=>E là trung điểm của AC
=>DI//CE và DI=CE
=>DICE là hình bình hành
c: Xét ΔABC có AD/AB=AE/AC
nên DE//BC
=>DE//IH
ΔHAC vuông tại H
mà HE là trung tuyến
nên HE=AC/2=DI
Xét tứ giác IHDE có
IH//DE
ID=HE
Do đó: IHDE là hình thang cân

a/
\(MP\perp AC;NA\perp AC\) => MP//NA
\(MN\perp AB;PA\perp AB\) => MN//PA
=> ANMP là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
Ta có \(\widehat{A}=90^o\)
=> ANMP là hình chữ nhật (hbh có 1 góc vuông là HCN)
b/
MN//PA (cmt) => MN//AC
MB=MC (gt)
=> NA=NB (trong tg đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại)
C/m tương tự cũng có PA=PC
Ta có
MP//NA (cmt) => MP//NB
NA=NB; PA=PC => NP là đường trung bình của tg ABC
=> NP//BC => NP//MB
=> BMPN là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
c/
Xét HCN ANMP có
FM=FA (trong HCN 2 đường chéo cắt nhau tại trung điểm mỗi đường)
EM=EB (gt)
=> EF là đường trung bình của tg MAB => EF//AB
=> ABEF là hình thang
Ta có
MB=MC => AM=MB=MC=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
Ta có
FM=FA=AM/2
EB=EM=BM/2
=> FA=EB
=> ABEF là hình thang cân
d/
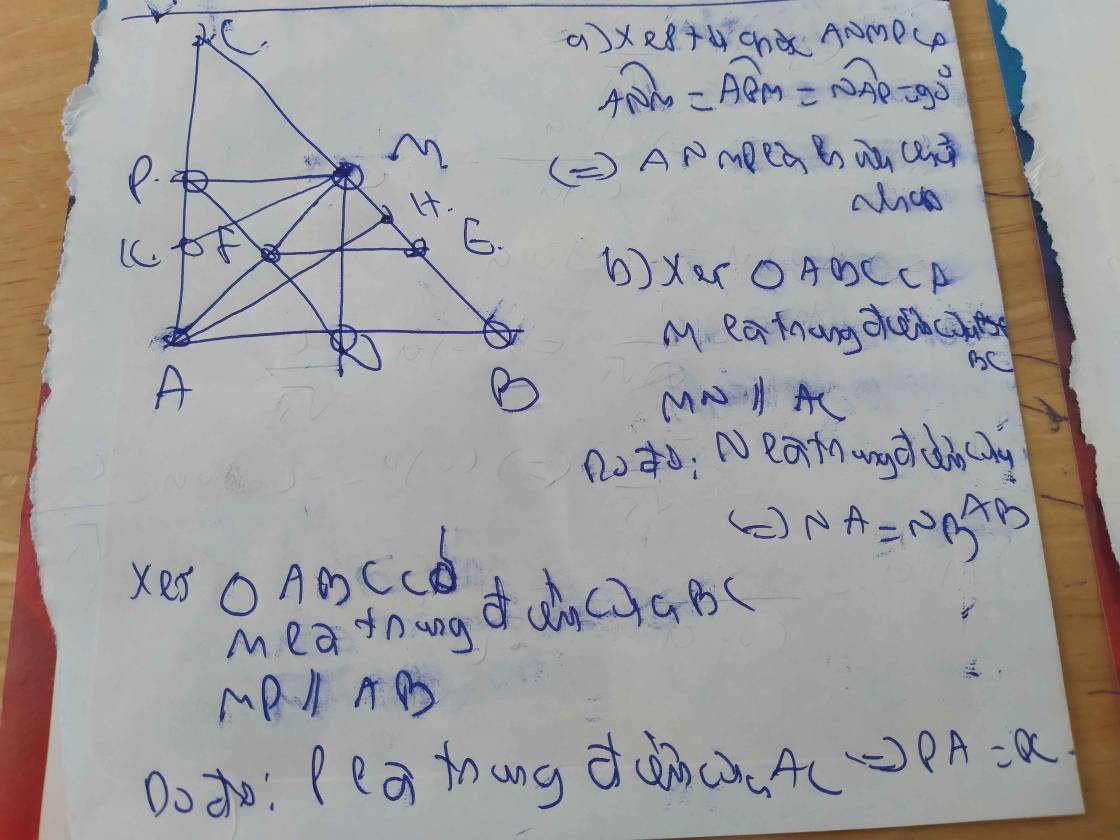



a,b ko khó nên bạn tự giải nha
c)Gọi O la giao điểm của NP và AM
=> O là trung điểm của AM và OM=OA=ON=OP
Xét tam giác AHM vuông tại H
Có O là td của AM (cmt)
=>HO la đường trung tuyến ứng với cạnh huyền AM
=>HO=OA=OM
mà OM=OA=OP=ON (cmt)
=>HO=OP=ON=1/2NP
Xét tam giác NHP
có HO=OP=ON=1/2NP(cmt)
=>tam giác NHP vuông tại H