Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cậu tự vẽ hình nha !
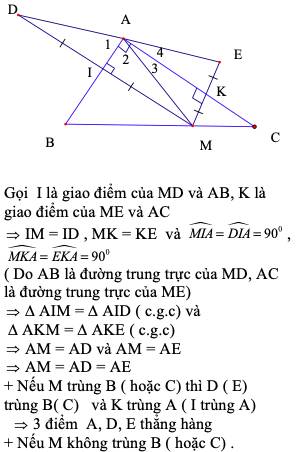
a) Vì AB là đường trung trực của DM
=> AD = AM (tính chất 1 điểm trên đường trung trực) (1)
Tương tự với AC là trung trực của ME
=> AM = AE (2)
Từ (1) và (2)
=> AM = AD = AE
b) Từ (1) ta suy ra \(\Delta ADM\) cân tại A
Từ (2) ta cũng có \(\Delta AEM\) cân tại A
Vì trong tam giác cân , đường trung trực , phân giác , trung tuyến , đường cao đều trung nhau
=> Với AB,AC là đường trung trực tương ứng thì AB,AC cũng là phân giác tương ứng
=> \(\widehat{DAB}=\widehat{MAB}=\frac{\widehat{MAD}}{2}\) và \(\widehat{MAC}=\widehat{CAE}=\frac{\widehat{MAE}}{2}\)
Ta có :
\(\widehat{BAM}+\widehat{MAC}=90^0\)
\(2\widehat{BAM}+2\widehat{MAC}=180^0\)
\(\widehat{MAD}+\widehat{MAE}=180^0\)
=> Ba điểm thẳng hàng

a: AC=8cm
Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
hay CB=CD
Xét ΔCBD có
DK là đường trung tuyến
CA là đường trung tuyến
DK cắt CA tại M
Do đó: M là trọng tâm
=>AM=AC/2=8/3(cm)
b: Xét ΔCAD có
G là trung điểm của AC
GQ//AD
Do đó: Q là trung điểm của CD
Vì M là trọng tâm của ΔCDB nên B,M,Q thẳng hàng