Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A

(tự vẽ hinh)
* Do AH vuông góc vs BC(gt)
=> Tam giác AHC và tam giác AHC là tam giác vuông tại H
* Tam giác vuông AHC có:
AC^2=AH^2+HC^2(ĐL py-ta-go)
20^2=12^2+HC^2
400=144+HC^2
HC^2=400-144
HC^2=256
HC^2=16^2(vì HC>0)
=>HC=16 cm
* Tam giác AHB có:
AB^2=AH^2+HB^2(DL py-ta-go)
AB^2=12^2+5^2
AB^2=144+25
AB^2=169
AB^2=13^2(vì AB>0)
=>AB=13 cm
*Ta có:
BH+HC=BC(AH vuống góc với BC tại H)
5+16=BC
=>BC=21cm
*Chu vi tam giác ABC:
AB+BC+AC=13+21+20=53cm
* Tam giác AHB và tam giác AHC là tam giác vuông trong vì:
AH vuông góc với BC tại H
AH cát BC tại hH tạo thành 2 tam giác vuông trong tam giác ABC

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC và AH là phân giác của góc BAC
=>góc BAH=góc CAH
b: \(BH=\sqrt{5^2-4^2}=3\left(cm\right)\)
c: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
góc DAH=góc EAH
Do đó: ΔADH=ΔAEH
=>AD=AE
=>ΔADE cân tại A

AB = 13 cm, BC = 21 cm.
Từ đó, chu vi của tam giác ABC là 54 cm.

A B H C
Xét \(\Delta\)AHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = \(\sqrt{256}\) = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét \(\Delta\)AHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = \(\sqrt{169}\) = 13 (cm)
Chu vi của \(\Delta\)ABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của \(\Delta\)ABC là 54 cm.

Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)

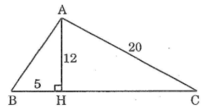
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

Ta có hình vẽ sau: A B H C 5cm 3cm 2,25 cm
Xét tam giác vuông ABH vuông tại H áp dụng định lí Pitago có:
AB^2 = BH^2 + AH^2
hay AB^2 = 3^2+2,25^2
= 9+ 5,0625 = 14,0625
=> AB = căn 14,0625 = 3,75 (cm)
=> chu vi của tam giác ABH là : AB+ AH+BH
hay 3,75+3+2,25 =9 (cm)
Xét tam giác vuông ABC vuông tại A áp dụng định lí Pitago có:
BC^2 = AB^2+AC^2
hay BC^2= 3,75^2+ 5^2
= 14,0625+ 25= 39,0625
=> BC= căn 39,0625= 6,25 (cm)
=> Chu vi của tam giác vuông ABC : AB+AC+ BC
hay 3,75+ 5+6,25= 15 (cm)
Xét tam giác vuông AHC vuông tại H áp dụng định lí PItago có:
AC^2= AH^2+ HC^2
hay 5^2 = 3^2 + HC^2
=> HC^2 = 5^2 - 3^2
= 25 - 9 =16 (cm)
=> HC= căn 16 =4 (cm)
=> Chu vi của tam giác vuông AHC : AH+AC+HC
hay 3+ 5+4=12 (cm)

Áp dụng định lí Pytago vào ΔAHC vuông tại H, ta được:
\(AC^2=AH^2+HC^2\)
\(\Leftrightarrow CH^2=AC^2-AH^2=5^2-3^2=16\)
hay CH=4(cm)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AB^2=3^2+2.25^2=14.0625\)
hay AB=3,75(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=2,25+4=6,25(cm)
Chu vi của tam giác ABH là:
\(C_{ABH}=AB+BH+HA=3.75+2.25+3=9\left(cm\right)\)
Chu vi của tam giác ACH là:
\(C_{ACH}=AC+CH+AH=5+3+4=12\left(cm\right)\)
Chu vi của tam giác ABC là:
\(C_{ABC}=AB+AC+BC=3.75+6.25+5=15\left(cm\right)\)