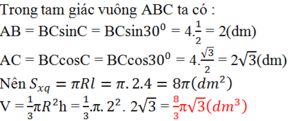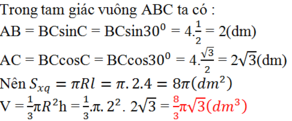Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

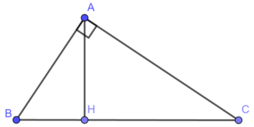
Đặt AB = c, AC = b, BC = a, AH = h là đường cao kẻ từ đỉnh A đến cạnh huyền BC
Vì tam giác ABC vuông tại A nên ta có: h = bc/a
*Khi quay tam giác vuông ABC một vòng quanh cạnh huyền BC thì cạnh AB và AC vạch nên hai hình nón chung đáy có bán kính đáy bằng đường cao AH và tổng chiều cao hai hình nón bằng cạnh huyền BC
Thể tích của hai hình nón:
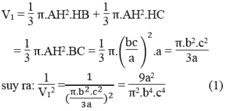
Khi quay tam giác vuông ABC một vòng quanh cạnh AB thì ta thu được hình nón có chiều cao AB = c, bán kính đáy AC = b
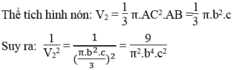
Khi quay tam giác vuông ABC một vòng quanh cạnh AC thì ta thu được hình nón có chiều cao AC=b,bán kính đáy AB=c
Thể tích hình nón:
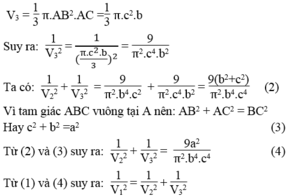

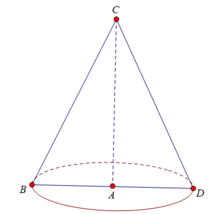
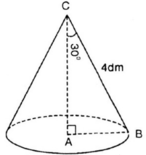
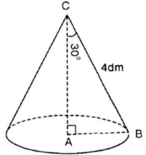
Xét tam giác ABC vuông tại A có: (ABC) = 60 0 , BC = 8 cm
⇒ AB = BC.cos (ABC) = 8.cos 60 0 = 4 (cm)
AC = BC.sin (ABC) = 8.sin 60 0 = 4 3 (cm)
Diện tích xung quanh của hình nón là
S x q = πrl = π.AB.BC = π.4.8 = 32 ( c m 2 )
Thể tích hình nón là:
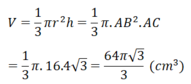

a: Xét ΔCKA vuông tại K có KI là đường cao ứng với cạnh huyền AC
nên \(CI\cdot CA=CK^2\left(1\right)\)
Xét ΔCKB vuông tại K có KH là đường cao ứng với cạnh huyền BC
nên \(CH\cdot CB=CK^2\left(2\right)\)
Từ (1) và (2) suy ra \(CI\cdot CA=CH\cdot CB\)

a: Xét ΔBDC có
DO là đường trung tuyến
DO=BC/2
Do đó: ΔBCD vuông tại D
=>CD\(\perp\)DB tại D
=>CD\(\perp\)AB tại D
Xét ΔBEC có
EO là đường trung tuyến
EO=BC/2
Do đó: ΔBEC vuông tại E
=>BE\(\perp\)EC tại E
=>BE\(\perp\)AC tại E
b: Xét ΔABC có
BE,CD là các đường cao
BE cắt CD tại K
Do đó: K là trực tâm của ΔABC
=>AK\(\perp\)BC