Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

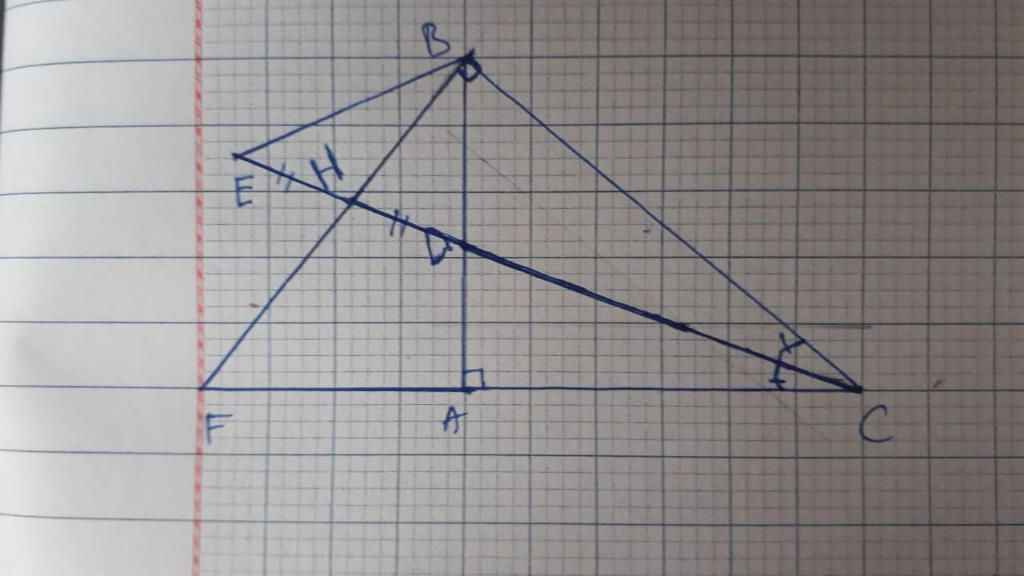
a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE

a) Xét ΔBDH vuông tại H và ΔBEH vuông tại H có
BH chung
DH=EH(H là trung điểm của DE)
Do đó: ΔBDH=ΔBEH(hai cạnh góc vuông)
Suy ra: \(\widehat{BDH}=\widehat{BEH}\)(hai góc tương ứng)
mà \(\widehat{BDH}=\widehat{ADC}\)(hai góc đối đỉnh)
và \(\widehat{CEB}=\widehat{BEH}\)
nên \(\widehat{CEB}=\widehat{ADC}\)(đpcm)
Ta có: ΔBDH=ΔBEH(cmt)
nên \(\widehat{DBH}=\widehat{EBH}\)(hai góc tương ứng)(1)
Xét ΔADC vuông tại A và ΔHDB vuông tại H có
\(\widehat{ADC}=\widehat{HDB}\)(hai góc đối đỉnh)
Do đó: ΔADC\(\sim\)ΔHDB(g-g)
Suy ra: \(\widehat{ACD}=\widehat{HBD}\)(hai góc tương ứng)(2)
Từ (1) và (2) suy ra \(\widehat{EBH}=\widehat{ACD}\)(Đpcm)

a,\(\Delta\)BED có H là trung điểm của DE và BH \(\perp\) DE
=> \(\Delta\)BED cân ở B
=> Góc BED = Góc BDE
Góc BDE = Góc ADC (đối đỉnh)
=> Góc BED = Góc ADC
\(\Delta\)BED cân ở B => BH là phân giác của góc EBD
=> gócEHB = gócDBH
mà gócDBH = 90⁰ - gócBFA = 90⁰ - gócHFC = gócACD
=> gócEBH = gócACD
b, gócEBH = gócACD = gócDCB (vì CH là phân giác của gócACB)
= 90⁰ - gócCBH
=> gócEHB + gócCBH = 90⁰
=> BE \(\perp\) BC
c, △FBC có CH \(\perp\) BF ; BA \(\perp\) FC ; CH \(\cap\) BA = D
=> D là trực tâm của \(\Delta\)FBC
=> FD \(\perp\) BC
BE \(\perp\) BC
=> FD//BE
1) a,△BED có H là trung điểm của DE và BH ┴ DE
=> △BED cân ở B
=> ∠BED = ∠BDE
∠BDE = ∠ADC (đối đỉnh)
=> ∠BED = ∠ADC
△BED cân ở B => BH là phân giác của ∠EBD
=> ∠EHB = ∠DBH
mà ∠DBH = 90⁰ - ∠BFA = 90⁰ - ∠HFC = ∠ACD
=> ∠EBH = ∠ACD
b, ∠EBH = ∠ACD = ∠DCB (vì CH là phân giác của ∠ACB)
= 90⁰ - ∠CBH
=> ∠EHB + ∠CBH = 90⁰
=> BE ┴ BC
c, △FBC có CH ┴ BF ; BA ┴ FC ; CH ⋂ BA = {D}
=> D là trực tâm của △FBC
=> FD ┴ BC
BE ┴ BC
=> FD//BE

tự vẽ hình nha
a) xét 2 tam giác BKA và CKD có:
BK=CK (K là TĐ của BC)
2 góc BKA=CKD (đối đỉnh)
KA=KD(gt)
=> 2 tam giác BKA=CKD(c.g.c) => góc ABK=góc DCK(2 góc tương ứng)
mà 2 góc này ở vị trí so le trong => AB//CD
b) 2 tam giác ABK=DCK(theo a) => BA=CD(2 cạnh tương ứng)
ta có AB//CD mà BA vuông góc với AC => DC vuông góc với AC
xét 2 tam giác ABH và CDH có:
góc BAH=góc DCH(=90độ)
BA=CD(chứng minh trên)
AH=CH(H là TĐ của AC)
=> 2 tam giác ABH=CDH(c.g.c)
2 tam giác ABH=CDH(theo b) => 2 góc AHB=CHD(2 góc tương ứng)
xét 2 tam giác BAC và DCA có:
góc BAC=góc DCA(=90độ)
BA=DC(2 tam giác BKA=CKD)
cạnh AC chung
=> 2 tam giác BAC=DCA(c.g.c) => 2 góc BCA=DAC(2 góc tương ứng)
xét 2 tam giác AMH và CNH có:
góc MAH =góc NCH (chứng minh trên )
HA=HC (H là TĐ của AC)
góc AHB = góc CHD( chứng minh trên)
=> 2 tam giác AMH =CNH(g.c.g) => MH=NH(2 cạnh tương ứng) => tam giác MHN cân ở H
c) Xem lại đề

a) Xét △MIA và △BIH có
MI=BI( giả thiết)
góc MIA =góc BIH(2 góc đối đỉnh)
IA=IH(Vì I là trung điểm của AH)
=> △MIA = △BIH(c-g-c)
=>góc IMA=góc IBH (2 góc tương ứng)
hay góc BMA=góc MBH mà 2 góc này là 2 góc so le trong của đường thẳng MB cắt MA và BH
=>MA//BH
bạn tự làm câu b,c nhé