Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

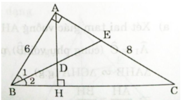
a) Ta có BE là phân giác của ∠ABC (gt)
⇒ ∠B1 = ∠B2
Do đó hai tam giác vuông:
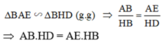
b) Ta có:
![]()
(định lý Pitago)
Xét hai tam giác vuông AHB và CAB có góc B chung nên :
![]()
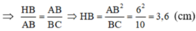
![]()


a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
Do đó: ΔHBA\(\sim\)ΔABC
b: \(\dfrac{S_{HBA}}{S_{ABC}}=\left(\dfrac{BA}{BC}\right)^2=\dfrac{9}{25}\)
c: \(BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=9.6\left(cm\right)\)
\(BH=\dfrac{AB^2}{BC}=7.2\left(cm\right)\)
CH=BC-BH=12,8(cm)

(mình k pk kẻ hình bn nhé)
ta có Scbe=1/2*AB*EC=1/2*ED*BC
suy ra AB.EC=BC.DE

4:
a: Xét ΔACH vuông tại H và ΔBCA vuông tại A có
góc ACH chung
=>ΔACH đồng dạng với ΔBCA
b: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>HA/HC=HB/HA
=>HA^2=HB*HC
c: góc EHD=góc EHA+góc DHA
=1/2*góc AHB+1/2*góc AHC=90 độ
góc EAD+góc EHD=180 độ
=>EADH nội tiếp
=>góc AED=góc AHD và góc ADE=góc AHE
mà góc AHD=góc AHE=45 độ
nên góc AED=góc ADE
=>AD=AE

d) Dễ thấy \(E\)là trực tâm của tam giác \(ACE\)(do là giao của hai đường cao \(DK,CH\)).
suy ra \(AE\perp CD\).
Để chứng minh \(BM//CD\)ta sẽ chứng minh \(AE\perp BM\).
Ta có:
\(\widehat{CAH}=\widehat{CBA}\)(vì cùng phụ với góc \(\widehat{ACB}\))
suy ra \(\widehat{CAE}=\widehat{ABM}\)
mà \(\widehat{CAE}+\widehat{EAB}=\widehat{CAB}=90^o\Rightarrow\widehat{ABM}+\widehat{EAB}=90^o\Rightarrow\widehat{AMB}=90^o\)
do đó \(BM\perp AE\).
Từ đây ta có đpcm.
Xét tam giacs ABE và HBD ta có:
Góc BAE = Góc BHD (=90^0)
Góc ABE = Góc HBD (GT)
=> Tam giacs ABE đồng dạng với tam giác HBD
\(\Rightarrow\dfrac{AB}{HB}=\dfrac{AE}{HD}\)
=> AB.HD = AE.HB