Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

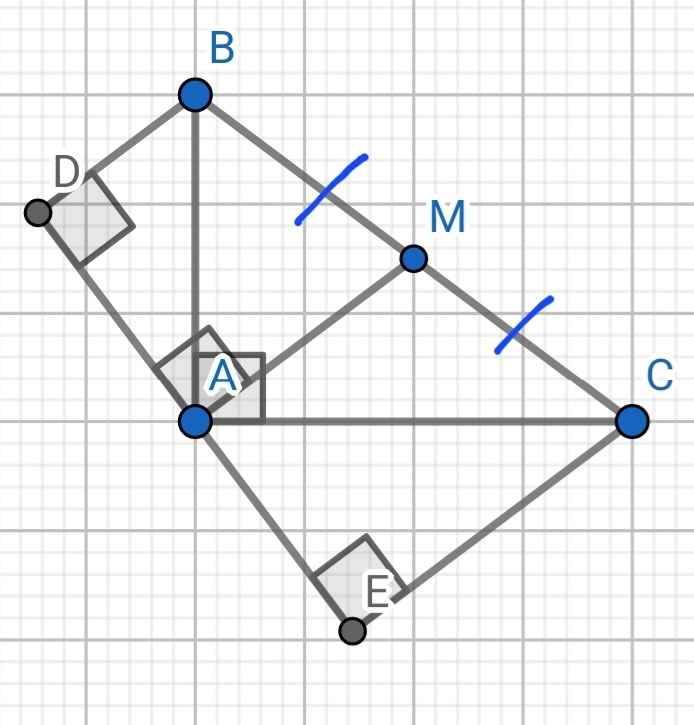
a) Sửa đề: Chứng minh ∆ABC ∽ ∆EAC
Giải:
∆ABC vuông tại A
⇒ BC² = AB² + AC² (Pytago)
= 6² + 8²
= 100
⇒ BC = 10 (cm)
Do AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
= 10 : 2 = 5 (cm)
∆AMC có AM = CM = 5 (cm)
⇒ ∆AMC cân tại M
⇒ ∠MAC = ∠MCA (hai góc ở đáy)
Do MA ⊥ DE (gt)
CE ⊥ DE (gt)
⇒ MA // DE
⇒ ∠MAC = ∠ACE (so le trong)
Mà ∠MAC = ∠MCA (cmt)
⇒ ∠MAC = ∠ACE
⇒ ∠ACE = ∠BCA (do ∠MAC = ∠BAC)
Xét hai tam giác vuông:
∆ABC và ∆EAC có:
∠BCA = ∠ACE (cmt)
⇒ ∆ABC ∽ ∆EAC (g-g)
b) Do ∆ABC ∽ ∆EAC (cmt)
⇒ AC/CE = BC/AC
⇒ CE = AC²/BC
= 8²/10
= 6,4 (cm)

Sửa đề: O là trung điểm của AD
a: Xét tứ giác BHCD có
BH//CD
BD//CH
Do đó; BHCD là hình bình hành
b: Vì BHCD là hình bình hành
nên BC cắt HD tại trung điểm của mỗi đường
=>M là trung điểm của HD
Xét ΔDAH co
M,O lần lượt là trung điểm của DH,DA
nên MO là đường trung bình
=>MO//AH và MO=1/2AH
=>AH=2MO

a: Xét tứ giác ADME có
\(\widehat{ADM}=\widehat{AEM}=\widehat{DAE}=90^0\)
=>ADME là hình chữ nhật
=>AM=DE
b: Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình
=>DE//BC và DE=1/2BC
=>DE//MC và DE=MC
Xét tứ giác DMCE có
DE//MC
DE=MC
Do đó: DMCE là hình bình hành
c: ΔHAC vuông tại H có HE là trung tuyến
nên \(HE=\dfrac{1}{2}AC\)
mà \(MD=\dfrac{1}{2}AC\)
nên HE=MD
Xét tứ giác DHME có
ED//MH
nên DHME là hình thang
mà HE=MD
nên DHME là hình thang cân
ΔHAB vuông tại H
mà HD là trung tuyến
nên HD=AD
EA=EH
DA=DH
Do đó: ED là đường trung trực của AH