Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/AC
=>DA/3=DC/5=(DA+DC)/(3+5)=8/8=1
=>DA=3cm; DC=5cm
b: IH/IA=BH/BA
AD/DC=BA/BC
mà BH/BA=BA/BC
nên IH/IA=AD/DC

Toán lớp 8 thì mik nghĩ bn vào lazi.vn hoặc hoc.24h.vn để hỏi nha
~ Hok tốt ~
#JH
a)
Xét tam giác ABC ta có
\(AB^2+AC^2=BC^2\)(định lý py ta go)
144 + 256 = BC2
400 = BC2
BC = 20 ( cm )
Xét tam giác ABC có
BD là đường phân giác của tam giác
nên AD/DC = AB/BC = 16/20 = 4/5
có AD + DC = AC = 16
dễ tìm ra AD = 64/9 (cm)
DC = 80/9 (cm)
b) xét 2 tam giác HBA và ABC
có góc ABC chung
2 góc AHB và CAB bằng nhau cùng bằng 90 độ
nên 2 tam giác HAB và ABC đồng dạng với nhau
c)
có 2 tam giác HAB và ABC đồng dạng với nhau
nên \(\frac{S_{HAB}}{S_{ABC}}=\left(\frac{AB}{BC}\right)^2=\left(\frac{12}{20}\right)^2=\frac{9}{25}\)
d)
có E là hình chiếu của của C trên BD
nên \(CE\perp BD\)
suy ra \(\widehat{BEC}=90^0\)
xét 2 tam giác BHK và BEC
có \(\widehat{BHK}=\widehat{BEC}=90^0\)
\(\widehat{CEB}\)chung
nên 2 tam giác BHK và BEC đồng dạng với nhau
suy ra \(\frac{BH}{BE}=\frac{BK}{BC}\Rightarrow BH\cdot BC=BK\cdot BE\)(1)
có 2 tam giác HAB và ABC đồng dạng với nhau
suy ra \(\frac{AB}{BC}=\frac{BH}{AB}\Rightarrow AB^2=BH\cdot BC\left(2\right)\)
từ (1) và (2) suy ra
\(AB^2=BK\cdot BE\)

a, Xét tam giác ABC và tam giác HBA ta có :
^BAC = ^AHB = 900
^B _ chung
Vậy tam giác ABC ~ tam giác HBA ( g.g )
c, tam giác ABC vuông tại A, có đường cao AH
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=36+64=100\Rightarrow BC=10\)cm
Ta có : \(\dfrac{AC}{AH}=\dfrac{BC}{AB}\)( cặp tỉ số đồng dạng ý a )
\(\Rightarrow\dfrac{8}{AH}=\dfrac{10}{6}\Rightarrow AH=\dfrac{48}{10}=\dfrac{24}{5}\)cm
d, phải là cắt AC nhé, xem lại đề nhé bạn

a: BC=căn 6^2+8^2=10cm
BF là phân giác
=>FA/AB=FC/BC
=>FA/3=FC/5=(FA+FC)/(3+5)=8/8=1
=>FA=3cm; FC=5cm
b: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>BA/BH=BC/BA
=>BA^2=BH*BC
b: AC=căn 15^2-9^2=12cm
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=12/8=1,5
=>AD=4,5cm; CD=7,5cm
c: góc AED=góc BEH=90 độ-góc DBC
góc ADE=90 độ-góc ABD
mà góc DBC=góc ABD
nên góc AED=góc ADE
=>ΔADE cân tại A
mà AI là trung tuyến
nên AI vuông góc ED
=>AI vuông góc BD
=>BI*BD=BA^2=BH*BC
=>BI/BC=BH/BD
=>ΔBIH đồng dạng với ΔBCD
=>góc BIH=góc C

a. Xét Δ HBA và Δ ABC:
\(\widehat{H}=\widehat{A}\) = 900 (gt)
\(\widehat{B}\) chung
\(\Rightarrow\) Δ HBA \(\sim\) Δ ABC (g.g)
Ta có: Δ HBA \(\sim\) Δ ABC
\(\dfrac{BA}{BC}=\dfrac{HB}{AB}\)
\(\Rightarrow AB^2=BH.BC\)
Ta có: \(\widehat{HAC}+\widehat{C}=90^0\)
mà \(\widehat{HAC}+\widehat{BAH}\) = 900
\(\Rightarrow\widehat{C}=\widehat{BAH}\)
Do E là đường phân giác \(\widehat{B}\)
\(\Rightarrow\widehat{ABE}=\widehat{EBC}\) hay \(\widehat{ABD}=\widehat{EBC}\)
Xét Δ ADB và Δ CEB:
\(\widehat{C}=\widehat{BAH}\)
\(\widehat{ABD}=\widehat{EBC}\)
\(\Rightarrow\) Δ ABD \(\sim\) Δ CEB (g.g)
c. Ta có: \(\widehat{AEB}=\widehat{ADE}\) hay \(\widehat{AED}=\widehat{ADE}\)
\(\Rightarrow\) Δ ADE là tam giác cân tại A
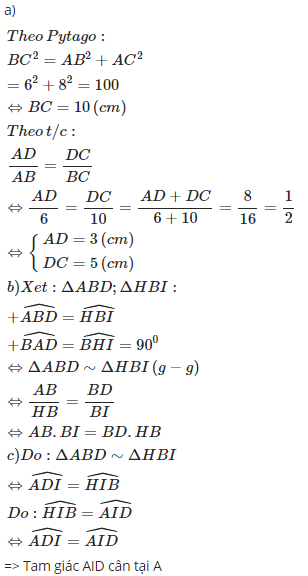

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/BC
=>DA/3=DC/5=(DA+DC)/(3+5)=8/8=1
=>DA=3cm; DC=5cm