Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABC vuông tại A có:
\(AB^2+AC^2=BC^2\left(pytago\right)\)
\(8^2+6^2=BC^2\left(64+36=100\right)\)
\(\Rightarrow BC=\sqrt{100}=10cm\)
b) Câu này viết lại đề đi

Xét tứ giác ABDC có
F là trung điểm chung của AD và BC
Do đó: ABDC là hình bình hành
=>BD=AC(1)
Xét ΔCAK có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCAK cân tại C
=>CA=CK(2)
Từ (1) và (2) suy ra BD=AC=CK
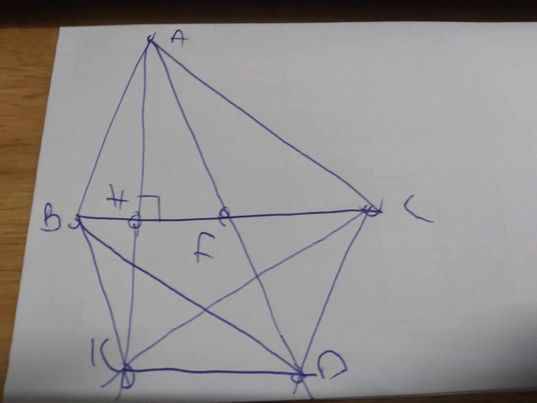

Xét ΔABF và ΔDCF có
FA=FD
\(\widehat{AFB}=\widehat{DFC}\)
FB=FC
Do đó: ΔABF=ΔDCF

F là trung điểm của BC
=>FB=FC
F là trung điểm của AD
=>AF=FD


a. Áp dụng định lý Pitago cho tam giác vuông ABC ta có: \(AC^2=BC^2-AC^2=10^2-6^2=64\)
Vậy \(AC=8cm\)
b. Do D nằm trên tia đối của tia AB nên \(\widehat{CAD}=90^O\)
Xét tam giác ABC và tam giác ADC có:
\(\widehat{CAB} = \widehat{CAD}=90^O\)
AC chung
AB=AD(giả thiết)
\(\Rightarrow\Delta ABC=\Delta ADC\)(Hai cạnh góc vuông)
c. Xét tam giác DCB có :
A là trung điểm BD,
AE song song BC
\(\Rightarrow\) AE là đường trung bình tam giác DBC., hay E là trung điểm DC. Vậy AE là đường trung tuyến ứng với cạnh huyền của tam giác vuông nên EA=EC=ED. Vậy tma giác AEC cân tại E. ( Còn có thể có cách khác :) )
d. Xét tam giác DBC có CA là trung tuyến, lại có CA = 3OA nên O là trọng tâm tam giác DBC. Do F là trung điểm BC nên DF là đường trung tuyến. Vậy O nằm trên DF hay O, D, F thẳng hàng.
Chúc em học tốt ^^
a)
Theo định lí py ta go trong tam giác vuông ABC có :
BC2 = AB2 + AC2
Suy ra : AC2 = BC2 - AB2
AC2 =102 - 62
AC = căn bậc 2 của 36 = 6 (cm )
b)
Xét tam giác ABC và tam giác ADC có :
AC cạnh chung
Góc A1 = góc A2 = 90 độ (gt )
AB = AD ( gt )
suy ra : tam giác ABC = tam giác ADC ( c- g -c )

a: AC=8cm
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: \(\widehat{ABD}=90^0\)
b: Xét ΔAMB và ΔDMC có
MA=MD
MB=MC
AB=DC
Do đó: ΔAMB=ΔDMC
Xét ΔABC và ΔBAD có
BA chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
c: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó AEDF là hình bình hành
Suy ra: HAi đường chéo AD và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của AD
nên M là trung điểm của FE
hay F,M,E thẳng hàng

Xét ΔAKD có
H,F lần lượt là trung điểm của AK,AD
Do đó: HF là đường trung bình của ΔAKD
=>HF//KD
Ta có: KD//HF
\(H,F\in BC\)
Do đó: KD//BC
Ta có: KD//BC
AH\(\perp\)BC
Do đó: AH\(\perp\)DK