Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh được ADCI là hình thoi.
b) Gọi AI Ç BN = G Þ là trọng tâm DABC.
Ta chứng minh DK = GI, lại có D C = A I ⇒ D K D C = G I A I = 1 3
c) SADCI = 2SACI = SABC = 96cm2

a)
Xét tam giác BAC vuông tại A và tam giác BMN vuông tại M có:
\(\widehat{BAC}\)=\(\widehat{BMN}\)
=> Tam giác BAC ᔕ Tam giác BMN (g-g)
=> BA/BM=BC/BN
=> BN=BM.\(\dfrac{BC}{BA}\)=18.\(\dfrac{20}{12}\)=30cm
b)
Xét tam giác PAN vuông tại A và tam giác PMC vuông tại M có
\(\widehat{APN}\)=\(\widehat{MPC}\) (đối đỉnh)
=> Tam giác PAN ᔕ Tam giác PMC (g-g)
=> \(\dfrac{PA}{PM}\)=\(\dfrac{PN}{PC}\)
=> PA.PC=PM.PN (đpcm)

a) tam giác BAC vuông tại A và tam giác BMN vuong tại M có: góc BAC=góc BMN
=> tam giác BAC đồng dạng tam giác BMN (g-g)
=> BA/BM=BC/BN=> BN=BM.BC/BA=18.20/12=30cm
b) tam giác PAN vuong tại A và tam giác PMC vuong tại M có
góc APN=góc MPC (đối đỉnh)
=> tam giác PAN đồng dạng tam giác PMC (g-g)
=> PA/PM=PN/PC
=> PA.PC=PM.PN (đpcm)
c) xét tam giác BNC có MN và AC là hai đường cao cắt nhau tại P
=> BP là đường cao thứ 3 kẻ từ B
=> BP vuong góc NC (đpcm)

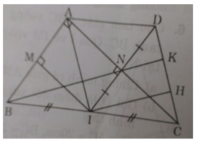
a) Xét tứ giác AMIN có:
∠(MAN) = ∠(ANI) = ∠(IMA) = 90o
⇒ Tứ giác AMIN là hình chữ nhật (có 3 góc vuông).
b) ΔABC vuông có AI là trung tuyến nên AI = IC = BC/2
do đó ΔAIC cân có đường cao IN đồng thời là đường trung tuyến
⇒ NA = NC.
Mặt khác ND = NI (t/c đối xứng) nên ADCI là hình bình hành
Lại có AC ⊥ ID (gt). Do đó ADCI là hình thoi.
c) Ta có: AB2 = BC2 – AC2 (định lí Py-ta-go)
= 252 – 202 ⇒ AB = √225 = 15 (cm)
Vậy SABC = (1/2).AB.AC = (1/2).15.20 = 150 (cm2)
d) Kẻ IH // BK ta có IH là đường trung bình của ΔBKC
⇒ H là trung điểm của CK hay KH = HC (1)
Xét ΔDIH có N là trung điểm của DI, NK // IH (BK // IH)
Do đó K là trung điểm của DH hay DK = KH (2)
Từ (1) và (2) ⇒ DK = KH = HC ⇒ DK/DC= 1/3.



Tam giác ABC vuông tại A, theo định lí Pi-ta-go ta có:
B C 2 = A B 2 + A C 2 ⇒ B C 2 = 5 2 + 12 2 = 169 ⇒ B C = 13
BM = 5 13 BC = 5 13 .13 = 5 => CM = 13 - 5 = 8.
Xét ΔCMN và ΔCBA có:
N = A = 90 ∘ (gt)
Góc C chung
=> ΔCMN ~ ΔCBA (g - g) => (cạnh tương ứng)
⇒ M N = A B . C M C B = 5.8 13 = 40 13
Đáp án: C