Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://coccoc.com/search?query=cho+tam+gi%C3%A1c+abc+vu%C3%B4ng+t%E1%BA%A1i+a+am+l%C3%A0+trung+tuy%E1%BA%BFn
Theo link nàyyy

https://coccoc.com/search?query=cho+tam+gi%C3%A1c+abc+vu%C3%B4ng+t%E1%BA%A1i+a+am+l%C3%A0+trung+tuy%E1%BA%BFn
#Theo link này nhoooo

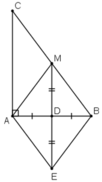
a) Ta có MB = MC, DB = DA
⇒ MD là đường trung bình của ΔABC
⇒ MD // AC
Mà AC ⊥ AB
⇒ MD ⊥ AB.
Mà D là trung điểm ME
⇒ AB là đường trung trực của ME
⇒ E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
⇒ AC = 2MD.
E đối xứng với M qua D
⇒ D là trung điểm EM
⇒ EM = 2.MD
⇒ AC = EM.
Lại có AC // EM
⇒ Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm ⇒ BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)- Cách 1:
Hình thoi AEBM là hình vuông ⇔ AB = EM ⇔ AB = AC
Vậy nếu ABC vuông có thêm điều kiện AB = AC (tức tam giác ABC vuông cân tại A) thì AEBM là hình vuông.
- Cách 2:
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM
⇔ ΔABC có trung tuyến AM là đường cao
⇔ ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

a) Ta có: E và M đối xứng với nhau qua D
=> DE = DM ; ME vuông góc AB
Ta có BD = DA ( D là trun điểm AB )
mà ME vuông góc AB ( cmt )
=> AB là trung trực của ME hay E và M đối xứng nhau qua D
b) Xét Tam giác ABC có:
M là trung điểm BC ( gt )
D là trung điểm AB ( gt)
=> DM là đường trung bình tam giác ABC
=> DM // AC; DM = 1/2AC
mà E thuộc DM
nên EM // AC
Xét tứ giác AEMC có:
EM // AC ( cmt)
EM = AC ( cùng = 2DM )
=> Tứ giác AEMC là hình bình hành( tứ giác có 2 cạnh đối vừa // vừa = nhau là hình bình hành)
c) Xét tứ giác AEBM có:
ED = DM ( gt )
DB = AD ( gt )
=> Tứ giác AEBM là hình bình hành ( D/h 5 )
mà AB vuông góc EM
=> hbh AEBM là hình thoi ( D/h 3 )
d) Ta có : AM = 1/2BC ( trung tuyến ứng với cạnh huyền)
=> AM = 1/2 . BC = 1/2. 5 = 2,5 (cm)
Chu vi hình thoi AEBM:
2,5 . 4 =10 (cm)
e) Nếu AEBM là hình vuông
thì Â= Ê= góc B= góc M= 90 độ
=>AM vuông góc BC
=> AM vừa là đường trung tuyến vừa là đường cao tam giác ABC
=> Tam giác ABC vuông cân tại A
Vậy tam giác ABC vuông cân ở A thì AEBM là hình vuông

a. Xét tứ giác AEBM có:
+ D là trung điểm AB (gt).
+ D là trung điểm EM (E là điểm đối xứng với M qua D).
\(\Rightarrow\) Tứ giác AEBM là hình bình hành (dhnb).
Mà AB \(\perp\) EM (E là điểm đối xứng với M qua D).
\(\Rightarrow\) Tứ giác AEBM là hình thoi (dhnb).
b. Tứ giác AEBM là hình thoi (cmt).
\(\Rightarrow\) AE = BM; AE // BM (tính chất hình thoi).
Ta có: M là trung điểm BC (AM là đường trung tuyến tam giác ABC).
\(\Rightarrow\) BM = CM.
Mà AE = BM (cmt).
\(\Rightarrow\) AE = CM.
Xét tứ giác AEMC có:
+ AE = CM (cmt).
+ AE // CM (AE // BM).
\(\Rightarrow\) Tứ giác AEMC là hình bình hành (dhnb).
c. Tứ giác AEBM là hình vuông (giả thiết).
\(\Rightarrow\) AM \(\perp\) BM (tính chất hình vuông).
\(\Rightarrow\) AM \(\perp\) BC.
Xét tam giác ABC vuông tại A có:
+ AM là đường trung tuyến tam giác ABC (gt).
Mà AM là đường cao (AM \(\perp\) BC).
\(\Rightarrow\) Tam giác ABC vuông cân tại A.
Vậy tam giác ABC vuông cân tại A thì AEBM là hình vuông.

a, M; D là trung điểm của AB, BC (gT)
=> MD là đường trung bình của tam giác ABC (đn)
=> MD // AC (đl)
=> góc BAC = góc MDB (đv)
góc BAC = 90 do
=> góc MDB = 90 và D là trung điểm của ME (gt)
=> M đx E qua AB
b, MD là đtb của tam giác ABC (Câu a)
=> MD = 1/2AC (Đl)
MD = DE do D là trung điểm của ME
=> MD + DE = 1/2AC + 1/2AC
=> ME = AC
có ME // AC (Câu a)
=> AEMC là hình bình hành
+có ME _|_ AB (Câu a)
=> AEBM là hình thoi
c, M là trung điểm của BC (gt)
=> MB = 1/2BC (tc)
BC = 4 cm (Gt)
=> MB = 1/2.4 = 2 (cm)
AEBM là hình thoi (Câu b) => AM = MB = ME = AE (đn)
=> C_AEBM =2.4 = 8 (cm)
d, Để AEBM là hình vuông
AEBM là hình thoi (Câu b)
<=> góc AMB = 90
<=> AM _|_ BC
AM là trung tuyến
<=> tam giác ABC vuông cân tại A
a) Ta có MB = MC, DB = DA
=> MD là đường trung bình của ΔABC
=> MD // AC
Mà AC ⊥ AB
=> MD ⊥ AB.
Mà D là trung điểm ME
=> AB là đường trung trực của ME
=> E đối xứng với M qua AB.
b) + MD là đường trung bình của ΔABC
=> AC = 2MD.
E đối xứng với M qua D
=> D là trung điểm EM
=> EM = 2.MD
=> AC = EM.
Lại có AC // EM
=> Tứ giác AEMC là hình bình hành.
+ Tứ giác AEBM là hình bình hành vì có các đường chéo cắt nhau tại trung điểm của mỗi đường.
Hình bình hành AEBM lại có AB ⊥ EM nên là hình thoi.
c) Ta có: BC = 4cm => BM = 2cm
Chu vi hình thoi AEBM bằng 4.BM = 4.2 = 8cm
d)
Hình thoi AEBM là hình vuông ⇔ AM ⊥ BM
<=> ΔABC có trung tuyến AM là đường cao
<=> ΔABC cân tại A.
Vậy nếu ΔABC vuông có thêm điều kiện cân tại A thì AEBM là hình vuông.

a: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến ứng với cạnh huyền BC
nên AM=BM=CM=BC/2
Xét tứ giác AMBE có
D là trung điểm của đường chéo AB
D là trung điểm của đường chéo ME
Do đó: AMBE là hình bình hành
mà AM=BM
nên AMBE là hình thoi
a, ta có E là điểm đối xứng với M qua D
=> me vuông góc vs md(t/c đối xứng)
xét tứ giác admn có
góc dan=90 độ
góc anm =90 độ
góc adm = 90 độ (d thuộc me)
=>tứ giác admn laf hcn
b,ta có d là trung điểm của ab
=>da=db(1)
lại có E là điểm đối xứng với M qua D
=> md=de(2)
từ 1 và 2 => từ giác aebm là hbh(3)
mà từ cma có me vuông góc vs md(t/c đối xứng)(4)
từ 3 và 4
=> từ giác aebm là hthoi
c, từ cmb có aebm là hthoi
=> ae=bm(t/c hthoi)
mà bm = cm =>ae=cm(1)
lại có da vuông góc cs me (t/c đối xứng), da vuông góc vs ac ( ab vuông góc vs ac, d thuộc ab)
=>me // ac (2)
từ 1 và 2 => tứ giác AEMC là hình bình hành
tcks cho nhé