Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
Xét ΔBAC có BD là phan giác
=>AD/AB=DC/BC
=>AD/3=DC/5=8/8=1
=>AD=3cm; DC=5cm
b: Xét ΔBAD vuông tại A va ΔBHI vuông tại H có
góc ABD=góc HBI
=>ΔBAD đồng dạng với ΔBHI
=>AD/HI=BA/BH
=>AD*BH=HI*BA
c: góc ADI=góc BIH=góc AID
=>ΔAID cân tại A

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=8/8=1
=>AD=3cm; CD=5cm
b: IH/IA=BH/BA
AD/CD=BA/BC
mà BH/BA=BA/BC
nên IH/IA=AD/CD

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/AC
=>DA/3=DC/5=(DA+DC)/(3+5)=8/8=1
=>DA=3cm; DC=5cm
b: IH/IA=BH/BA
AD/DC=BA/BC
mà BH/BA=BA/BC
nên IH/IA=AD/DC

a: BC=10cm
Xét ΔABC có BD là phân giác
nên AD/DC=AB/BC(1)
=>AD/AB=DC/BC
=>AD/6=DC/10
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{6}=\dfrac{DC}{10}=\dfrac{AD+DC}{6+10}=\dfrac{8}{16}=\dfrac{1}{2}\)
Do đó:AD=3cm; DC=5cm
b: Xét ΔABH có BI là phân giác
nên IH/IA=BH/BA(2)
Xét ΔABH vuông tại H và ΔCBA vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔABH∼ΔCBA
Suy ra: BH/BA=BA/BC(3)
Từ (1), (2) và (3) suy ra IH/IA=AD/DC

a, Xét tam giác ABC vuông tại A, có AH là đường cao
Áp dụng định lí Py ta go ta có :
\(BC^2=AB^2+AC^2=36+64\)
\(\Rightarrow BC^2=100\Rightarrow BC=10\)cm
Vì BD là phân giác ^ABC nên
\(\frac{AB}{BC}=\frac{AD}{DC}\)(1) mà \(AD=AC-DC=8-DC\)
hay \(\frac{6}{10}=\frac{8-DC}{DC}\Rightarrow6DC=80-10DC\)
\(\Leftrightarrow16DC=80\Leftrightarrow DC=5\)cm
\(\Rightarrow AD=AC-DC=8-5=3\)cm
b, Xét tam giác BHA và tam giác BAC ta có
^BHA = ^A = 900
^B _ chung
Vậy tam giác BHA ~ tam giác BAC ( g.g )
\(\Rightarrow\frac{BH}{BA}=\frac{AB}{BC}\) ( tỉ số đồng dạng ) (2)
Từ (1) và (2) \(\Rightarrow\frac{BH}{BA}=\frac{AD}{DC}\)(3)
xem lại đề đi nếu như thành \(\frac{IH}{AD}=\frac{IA}{DC}\)
sao lại có tam giác IHA được ? hay còn cách nào khác ko ?

a: BC=10cm
Xét ΔBAC có BD là phân giác
nên AD/AB=CD/BC
=>AD/3=CD/5
Áp dụng tính chất của dãy tỉ sốbằng nhau, ta được:
AD/3=CD/5=(AD+CD)/(3+5)=8/8=1
=>AD=3cm; CD=5cm
b: Xét ΔBAD vuông tại A và ΔBHI vuông tại H có
góc ABD=góc HBI
Do đó:ΔBAD đồng dạng với ΔBHI
Suy ra: BA/BH=BD/BI
hay \(BA\cdot BI=BH\cdot BD\)
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
mà góc DBC=góc ABD
nên góc AID=góc ADI
hay ΔAID cân tại A

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
AD/DC=BA/BC=6/10=3/5
b: Xét ΔHBA vuông tạiH và ΔABC vuôg tại A có
góc B chung
=>ΔHBA đồng dạng với ΔABC
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
màgóc DBC=góc ABD
nên góc AID=góc ADI
=>ΔAID cân tại A
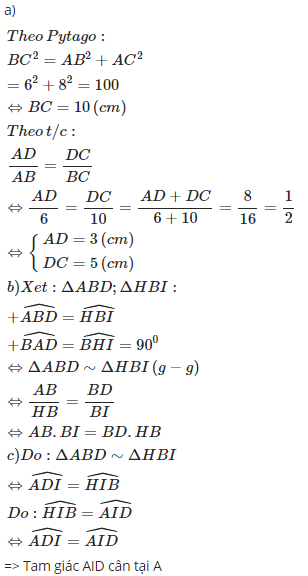
Aps dụng tích chất đường phân giác trong tam giác ABC ta có :
\(\frac{ad}{dc}=\frac{ab}{bc}\)( T/C đường phân giác )
Aps dụng tính chất đường phân giác trong tam giác ABH ta có :
\(\frac{oh}{oa}=\frac{ab}{ac}\) ( tích chất đường phân giác )
từ hai điều trên suy ra : \(\frac{ho}{ao}=\frac{ad}{dc}\)