Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

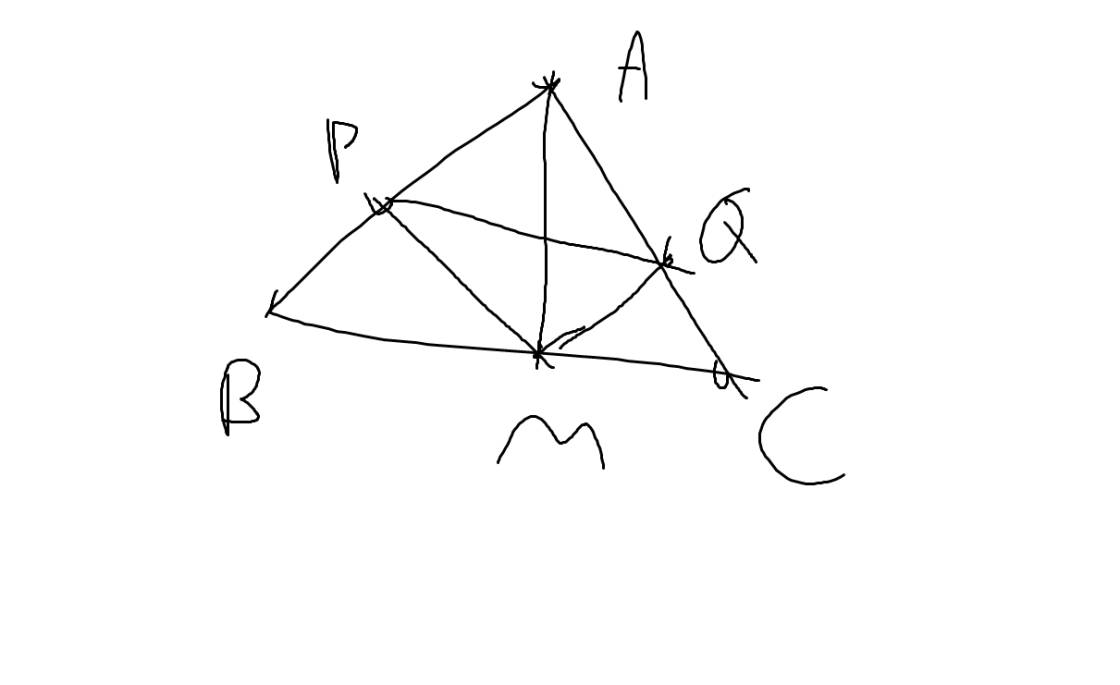
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔPAM vuông tại P và ΔQAM vuông tại Q có
AM chung
\(\widehat{PAM}=\widehat{QAM}\)
Do đó: ΔPAM=ΔQAM
=>PA=QA và MP=MQ
b: AP=AQ
=>A nằm trên đường trung trực của PQ(1)
MP=MQ
=>M nằm trên đường trung trực của PQ(2)
Từ (1) và (2) suy ra AM là đường trung trực của PQ
=>AM\(\perp\)PQ

Bạn kiểm tra lại đề nhé! Tia Ax nằm giữa hai tia AD và AC hay hai tia AB và AC
Tham khảo đề bài và lời giải tại link:
Câu hỏi của Chử Văn Dũng - Toán lớp 7 - Học toán với OnlineMath

a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔABM=ΔACM
b: ΔABM=ΔACM
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
=>KM\(\perp\)BC
Xét ΔKBC có
KM là đường cao
KM là đường trung tuyến
Do đó:ΔKBC cân tại K
=>KB=KC
c: ΔKBC cân tại K
=>\(\widehat{KBC}=\widehat{KCB}\)
\(\widehat{ABF}+\widehat{FBC}=\widehat{ABC}\)
\(\widehat{ACE}+\widehat{ECB}=\widehat{ACB}\)
mà \(\widehat{FBC}=\widehat{ECB}\)
và \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{ABF}=\widehat{ACE}\)
=>\(\widehat{EBK}=\widehat{FCK}\)
Xét ΔEBK và ΔFCK có
\(\widehat{EBK}=\widehat{FCK}\)
BK=CK
\(\widehat{EKB}=\widehat{FKC}\)
Do đó: ΔEBK=ΔFCK

a) Vì AM là phân giác của góc BAC
nên góc BAM = CAM
Xét ΔBAM và ΔCAM có:
AB = AC ( giả thiết )
Góc BAM = CAM ( chứng minh trên )
AM cạnh chung.
=> Δ BAM = ΔCAM ( c.g.c )
=> BM = CM ( 2 cạnh tương ứng )
mà M nằm giữa B và C
Do đó M là trung điểm của BC → ĐPCM.
b) Ta có: AB + BE = AE
AC + CF = AF
mà AB = AC ( đề bài ); AE = AF (đề bài)
=> BE = CF.
Do ΔBAM = ΔCAM nên góc ABC = ACB ( 2 góc tương ứng )
Lại có: Góc ABC + CBE = 180 độ (kề bù)
Góc ACB + BCF = 180 độ (kề bù)
=> ABC + CBE = ACB + BCF
=> Góc CBE = BCF.
Xét ΔBCE và ΔCBF có:
BE = CF ( chứng minh trên)
Góc CBE = BCF ( chứng minh trên)
BC cạnh chung ( theo hình vẽ)
=> ΔBCE = ΔCBF ( c.g.c ) → ĐPCM.
c) Lại do ΔBCE = ΔCBF nên góc EBC = FCB ( 2 góc tương ứng ) hay góc EBM = FCM
Xét ΔMBE và ΔMCF có:
MB = MC ( chứng minh ở câu a )
Góc EBM = FCM ( chứng minh trên)
BE = FC ( chứng minh ở câu b)
=> ΔMBE = ΔMCF ( c.g.c )
=> ME = MF ( 2 cạnh tương ứng ) → ĐPCM.
d) Xét ΔEMN và ΔFMN có:
EM = FM ( chứng minh ở câu c )
EN = FN ( N là trung điểm EF )
MN chung.
=> ΔEMN = ΔFMN.
=> Góc ENM = FNM (2 góc tương ứng)
Suy ra MN là tia phân giác của góc ENF (1)
Có: góc BAM = CAM
Suy ra AM là tia phân giác của góc BAC (2)
Từ (1) và (2) suy ra A, M, N nằm trên cùng 1 đường thẳng.
Do đó A, M, N thẳng hàng → ĐPCM.
