Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là phân giác của góc BAC và AH\(\perp\)BC
Xét tứ giác AHCE có
I là trung điểm chung của AC và HE
=>AHCE là hình bình hành
Hình bình hành AHCE có \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
=>AE//CH và AE=CH
Ta có: AE//CH
H\(\in\)BC
Do đó: AE//HB
Ta có: AE=CH
CH=HB
Do đó: AE=HB
Xét tứ giác AEHB có
AE//HB
AE=HB
Do đó: AEHB là hình bình hành
c: Xét ΔABC có
H,I lần lượt là trung điểm của CB,CA
=>HI là đường trung bình của ΔABC
=>HI//AB và HI=AB/2
Ta có: HI//AB
K\(\in\)AB
Do đó: HI//AK
Ta có: HI=AB/2
AK=KB=AB/2
Do đó: HI=AK=KB
Xét tứ giác AKHI có
HI//AK
HI=AK
Do đó: AKHI là hình bình hành
Hình bình hành AKHI có AH là phân giác của góc KAI
nên AKHI là hình thoi
c: Để hình chữ nhật AHCE trở thành hình vuông thì AH=CH
mà \(CH=\dfrac{CB}{2}\)
nên \(AH=\dfrac{CB}{2}\)
Xét ΔABC có
AH là đường trung tuyến
\(AH=\dfrac{CB}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)

a, tứ giác AHCE là hình chữ nhật , vì AD=DC và HD=DE
b, áp dụng đl pytago vào tam giác vuông AHC( H là đường cao ABC):
\(HC^2=AC^2-AH^2\\ HC^2=10^2-6^2\\ HC=\sqrt{10^2-6^2}=8cm\)
\(S_{AHCE}=AH.HC=6.8=48cm^2\)

sai đề rồi cậu ơi! I là trung điểm của AC rồi đằng sau I còn là trung điểm của HC, CE

a: Xét tứ giác AHCE có
D là trung điểm của AC
D là trung điểm của HE
Do đó: AHCE là hình bình hành
mà \(\widehat{AHC}=90^0\)
nên AHCE là hình chữ nhật
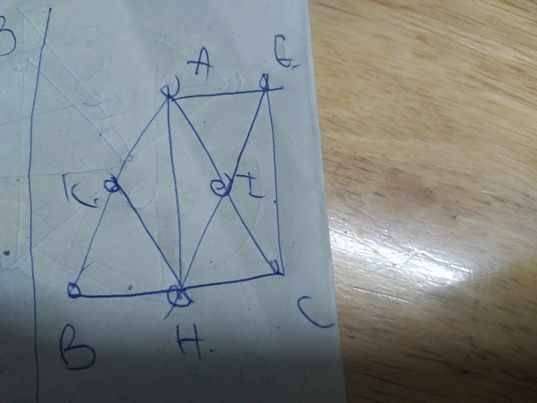
a: Xét tứ giác AHCE có
I là trung điểm chung của AC,HE
góc AHC=90 độ
HA=HC
=>AHCE là hình vuông
b: Để AHCE là hình vuông thì ΔABC cần có những điều kiện sau:
AB=AC; góc B=45 độ