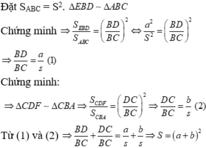Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) ED // BF; FE // BD => Tứ giác FBDE là hbh => DE = BF
+) Dễ có: tam giác ADE đồng dạng với ABC => \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{DE}{BC}\right)^2\) (*) ( tỉ số diện tích = bình phương tỉ số đồng dạng)
Tam giác CFE đồng dạng với tam giác CAB => \(\frac{S_{CFE}}{S_{ABC}}=\left(\frac{CF}{BC}\right)^2\)
=> \(\frac{S_{ADE}}{S_{ABC}}:\frac{S_{CFE}}{S_{ABC}}=\left(\frac{DE}{BC}\right)^2:\left(\frac{CF}{CB}\right)^2\) => \(\frac{S_{ADE}}{S_{CFE}}=\left(\frac{DE}{FC}\right)^2=\frac{101}{143}\) => \(\left(\frac{BF}{CF}\right)^2=\frac{101}{143}\)
=> \(\frac{BF}{CF}=\sqrt{\frac{101}{143}}\) => \(\frac{BF}{CF+BF}=\frac{\sqrt{101}}{\sqrt{143}+\sqrt{101}}\)=> \(\frac{BF}{BC}=\frac{\sqrt{101}}{\sqrt{143}+\sqrt{101}}=\frac{DE}{BC}\)
Thay vào (*) => \(\frac{S_{ADE}}{S_{ABC}}=\left(\frac{\sqrt{101}}{\sqrt{101}+\sqrt{143}}\right)^2=\frac{101}{S_{ABC}}\) => S(ABC) =....

Đặt \(S_{ABC}=x^2\)
Ta có :
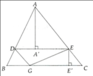
+) \(MD//AC\Leftrightarrow\frac{S_{BMD}}{S_{ABC}}=\left(\frac{BM}{BC}\right)^2\)
\(\Leftrightarrow\frac{a^2}{x^2}=\frac{BM^2}{BC^2}\)
\(\Leftrightarrow\frac{a}{x}=\frac{BM}{BC}\) (1)
+) \(ME//AB\Leftrightarrow\frac{S_{CEM}}{S_{ABC}}=\left(\frac{MC}{BC}\right)^2\)
\(\Leftrightarrow\frac{b^2}{x^2}=\frac{CM^2}{BC^2}\)
\(\Leftrightarrow\frac{b}{x}=\frac{CM}{BC}\) (2)
Từ (1) và (2) suy ra :
\(\frac{a+b}{x}=\frac{CM+MB}{BC}=1\)
\(\Leftrightarrow x=a+b\)
\(\Leftrightarrow S_{ABC}=x^2=\left(a+b\right)^2\)