Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Từ $M$ kẻ \(MG\parallel AB(G\in EC)\)
Áp dụng định lý Thales:
\(\frac{BC}{MC}=\frac{EB}{GM}\) và \(\frac{MI}{AI}=\frac{GM}{AE}\)
Nhân hai biểu thức với nhau:
\(\frac{BC}{MC}.\frac{MI}{AI}=\frac{EB}{AE}\)
\(\Leftrightarrow \frac{EB}{AE}=2.1=2\)
\(\Leftrightarrow \frac{BE}{AB}=\frac{2}{3}\)
Do đó:\(\frac{S_{CEB}}{S_{ABC}}=\frac{EB}{AB}=\frac{2}{3}\Rightarrow S_{CEB}=\frac{2}{3}.36=24\)
\(\frac{S_{BFC}}{S_{BEC}}=\frac{BF}{BE}=\frac{1}{2}\Rightarrow S_{BFC}=\frac{1}{2}S_{BEC}=12\) (mét vuông)

FM là đường trung bình của \(\Delta BEC\Rightarrow FM//EC\)
\(\Delta AFM\) có I là trung điểm của AM và EI // FM nên E là trung điểm của AF \(\Rightarrow AE=EF\)
Mà EF = FB \(\Rightarrow AE=EF=FB=\frac{1}{3}AB\)
Tam giác BFC và BAC có chung chiều cao hạ từ đỉnh C và \(FB=\frac{1}{3}AB\Rightarrow S_{BFC}=\frac{1}{3}S_{BAC}=\frac{1}{3}.36=12\left(cm^2\right)\)
\(\)


Do ME là đường trung bình của tam giác BDC nên \(ME//DC\)
Mặt khác I là trung điểm của AM;\(DI//EM\Rightarrow DE=DA\)
Mà \(ME=ED\) vì E trung điểm.
Vậy \(AD=DE=EB\)
Bổ sung chút cho bài của bạn Cood Kid
Gọi E là trung điểm BD
Xét tam giác BCD có M là trung điểm BC, E là trung điểm BD
=> ME là đường trung bình của tam giác BCD.

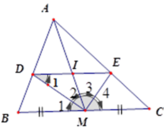
Vì DI = IE (cmt) nên MI là đường trung tuyến của tam giác MDE.
ΔMDE vuông (vì MD, ME là tia phân giác của góc kề bù) nên MI = DI = IE
Đặt DI = MI = x, ta có D I B M = A I A M (cmt) nên x 15 = 10 − x 10
Từ đó x = 6 suy ra DE = 12cm
Đáp án: D