Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

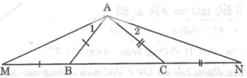
Trong ΔAMN, ta có: ∠(AMB) > ∠(ANC)
Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).

Trong \(\Delta ABC\)có: \(AB=AC\) (gt)
\(\Rightarrow\Delta ABC\)cân tại A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(2 góc đáy)
Mà \(\widehat{ABC}+\widehat{ABM}=180^o\)
\(\widehat{ACB}+\widehat{ACN}=180^o\)
Nên \(\widehat{ABM}=\widehat{ACN}\)
Xét \(\Delta ABM\)và \(\Delta ACN\)có:
\(AB=AC\)(gt)
\(\widehat{ABM}=\widehat{ACN}\)(chứng minh trên)
\(MB=NC\)(gt)
Do đó \(\Delta ABM=\Delta ACN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\)

a: Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
Do đó: ΔAIB=ΔAIC

a: Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
b:
Xét ΔABM và ΔACN có
AB=AC
\(\widehat{ABM}=\widehat{ACN}\)
BM=CN
Do đó: ΔABM=ΔACN
=>AM=AN
=>ΔAMN cân tại A
c: Ta có: ΔABC cân tại A
=>\(\widehat{ABC}\) nhọn
=>\(\widehat{ABM}=180^0-\widehat{ABC}>90^0\)
Xét ΔABM có \(\widehat{ABM}>90^0\)
mà AM là cạnh đối diện của góc ABM
nên AM là cạnh lớn nhất trong ΔABM
=>AM>AB
mà AB=AC
nên AM>AC