Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay \(BC=13cm\)
Vậy: BC=13cm
b) XÉT ΔABE VÀ ΔDBE ,CÓ
BD=BA (B LÀ TRUNG ĐIỂM CỦA AD)
\(\widehat{DBE}=\widehat{ABE}\) =90
EB : CẠNH CHUNG
⇒ΔABE = ΔDBE (C-G-C)

Bạn tự vẽ hình nha.
a, Áp dụng Đ. L. py-ta-go vào tg ABC vuông tại A, có:
BC2=AC2+AB2
=>BC2=122+52
=144+25
=169.
=>BC=13cm.
b, Xét tg ABE và tg DBE, có:
BE chung
góc DBE= góc ABE(=90o)
AB=BD(B là trung điểm của AD)
=>tg DBE= tg ABE(2 cạnh góc vuông)
=>AD=ED(2 cạnh tương ứng)
=>tg ADE là tg cân tại E.
c, Xét tg BDF và tg BKA, có:
góc BDF= góc ABK(2 góc đối đỉnh)
DB=BD(B là trung điểm của AD)
góc DFB= góc BKA(=90o)
=>tg DFB= tg AKB(ch-gn)
=>FB=BK(2 cạnh tương ứng)
=>B là trung điểm của KF.
d, Ta có: góc DBE= góc ABE. Mà 2 tg AEB và tg DEB bằng nhau.
=>EB là tia phân giác của góc DEA.
Vì góc DAC= góc DBE(=90o) và 2 góc này ở vị trí đồng vị, suy ra:
BE // AC.
=>góc DEB= góc ECA( đồng vị)
=> góc BEA= góc EAC(SLT)
Mà góc DEB= góc BEA(BE là tia phân giác của góc DEA)
=>góc EAC= góc ECA.
=>tg AEC là tg cân tại E.
=>AE=EC.
Ta có: DE=EA(2 cạnh tương ứng)
AE=EC(cmt)
=>DE=EC.
=>E là trung điểm của DC(đpcm)

a: BC=căn 5^2+12^2=13cm
b: Xét ΔABE vuông tại B va ΔDBE vuông tại B có
BE chung
BA=BD
=>ΔABE=ΔDBE
=>EA=ED
=>ΔEAD cân tại E
c: Xét ΔBKA vuông tại K và ΔBFD vuông tại F có
BA=BD
góc ABK=góc DBF
=>ΔBKA=ΔBFD
=>BK=BF
=>B là trung điểm của KF
d: góc EAD+góc EAC=90 độ
góc EDA+góc ECA=90 độ
mà góc EAD=góc EDA
nên góc EAC=góc ECA
=>ΔEAC cân tại E
=>EA=EC=ED
=>E là trung điểm của DC

a: BC=13cm
b: Xét ΔABE vuông tại B và ΔDBE vuông tại B có
BA=BD
BE chung
Do đó: ΔABE=ΔDBE
Suy ra: AE=DE
hay ΔAED cân tai E

Bài 5:
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+12^2=169\)
hay BC=13(cm)
Vậy: BC=13cm
b) Xét ΔABE vuông tại B và ΔDBE vuông tại B có
EB chung
BA=BD(B là trung điểm của AD)
Do đó: ΔABE=ΔDBE(hai cạnh góc vuông)
Suy ra: EA=ED(Hai cạnh tương ứng)
Xét ΔEAD có EA=ED(cmt)
nên ΔEAD cân tại E(Định nghĩa tam giác cân)

a: BC=13cm
b: Xét ΔABE vuông tại B và ΔDBE vuông tại B có
BE chung
BA=BD
Do đó: ΔABE=ΔDBE
Suy ra: EA=ED
hay ΔEAD cân tại E
c: Xét ΔAKB vuông tại K và ΔDFB vuông tại F có
BA=BD
\(\widehat{ABK}=\widehat{DBF}\)
Do đó: ΔAKB=ΔDFB
Suy ra: BK=BF
hay B là trung điểm của KF

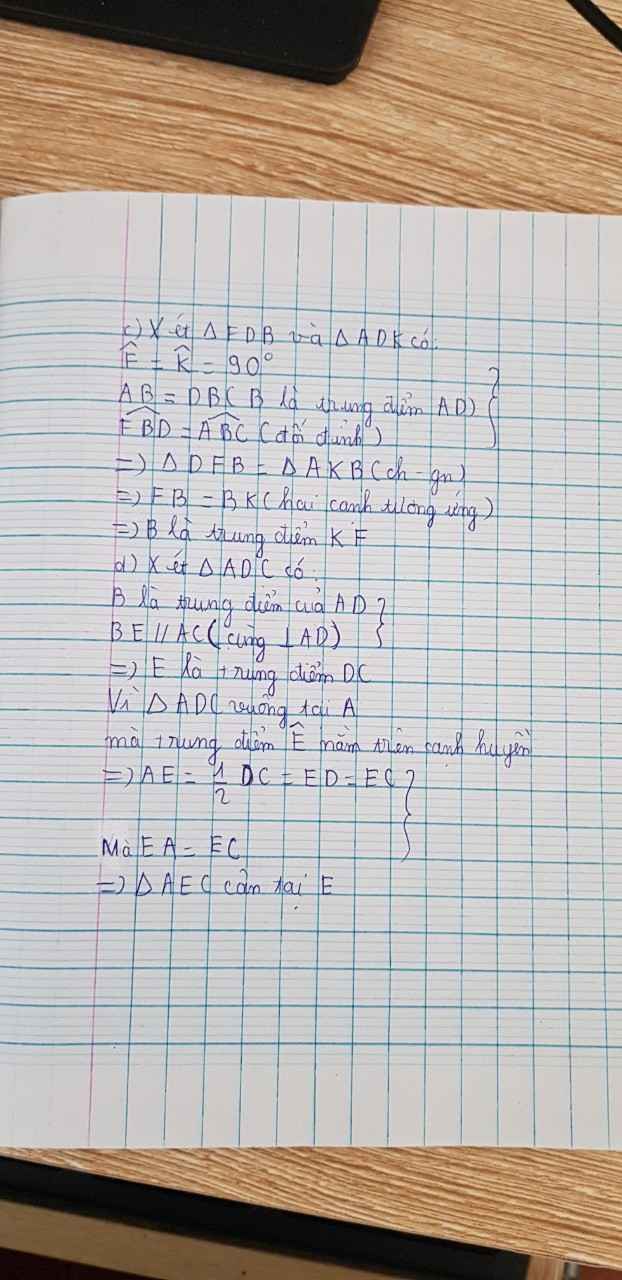

Nối A với D
Sabg=Sbgd(chung đường cao kẻ từ b, ag=gd)
tương tự: Sagk=Skga
=>Sagk+Sagb=Sbgd+Skdg
=>Sabk=SKbd
Skbd=2/5Skbc(chung đường cao kẻ từ K và bd=2/5bc)
=>Sabk=2/5Skbc
=>ak=2/5kc
=>ak=2/7ac