TT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
5 tháng 11 2023
Ta có:
\(\dfrac{tanA}{tan^3B}=\dfrac{tanA}{tanB}.\dfrac{1}{tan^2B}=\dfrac{\dfrac{sinA}{cosA}}{\dfrac{sinB}{cosB}}.\dfrac{cos^2B}{sin^2B}\)
\(=\dfrac{sinA}{sinB}.\dfrac{cosB}{cosA}.\dfrac{cos^2B}{sin^2B}\)
\(=\dfrac{a}{b}.\dfrac{\dfrac{a^2+c^2-b^2}{2ac}}{\dfrac{b^2+c^2-a^2}{2bc}}.\dfrac{\left(\dfrac{a^2+c^2-b^2}{2ac}\right)^2}{1-\left(\dfrac{a^2+c^2-b^2}{2ac}\right)^2}\)
\(=\dfrac{a^2+c^2-b^2}{b^2+c^2-a^2}.\dfrac{\left(a^2+c^2-b^2\right)^2}{\left(2ac\right)^2-\left(a^2+c^2-b^2\right)^2}\)
\(=\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}.\dfrac{1}{\left[\left(a+c\right)^2-b^2\right]\left[b^2-\left(a-c\right)^2\right]}\)
\(=\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}.\dfrac{1}{\left(a+b+c\right)\left(a+c-b\right)\left(b+c-a\right)\left(a+b-c\right)}\)
Biến đổi tương tự, ta có BĐT tương đương với BĐT đã cho:
\(\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}+\dfrac{\left(a^2+b^2-c^2\right)^3}{a^2+c^2-b^2}+\dfrac{\left(b^2+c^2-a^2\right)^3}{a^2+b^2-c^2}\ge\left(a+b+c\right)\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)\)
Ta có BĐT phụ sau:
\(\dfrac{x^3}{y}+\dfrac{y^3}{z}+\dfrac{z^3}{x}\ge xy+yz+xz\left(\text{*}\right)\) với \(x,y,z>0\)
Chứng minh:
Áp dụng BĐT cộng mẫu:
\(\dfrac{x^3}{y}+\dfrac{y^3}{z}+\dfrac{z^3}{x}=\dfrac{x^4}{xy}+\dfrac{y^4}{yz}+\dfrac{z^4}{xz}\)
\(\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{xy+yz+xz}\ge\dfrac{\left(xy+yz+xz\right)^2}{xy+yz+xz}=xy+yz+xz\)(đpcm)
Đẳng thức xảy ra khi và chỉ khi \(x=y=z\)
Áp dụng BĐT \(\left(\text{*}\right)\), với đk \(\Delta ABC\) có ba góc nhọn, ta có:
\(\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}+\dfrac{\left(a^2+b^2-c^2\right)^3}{a^2+c^2-b^2}+\dfrac{\left(b^2+c^2-a^2\right)^3}{a^2+b^2-c^2}\ge\left(a^2+c^2-b^2\right)\left(a^2+b^2-c^2\right)+\left(a^2+b^2-c^2\right)\left(b^2+c^2-a^2\right)+\left(b^2+c^2-a^2\right)\left(a^2+c^2-b^2\right)\)
Ta chứng minh được:
\(\left(a^2+c^2-b^2\right)\left(a^2+b^2-c^2\right)+\left(a^2+b^2-c^2\right)\left(b^2+c^2-a^2\right)+\left(b^2+c^2-a^2\right)\left(a^2+c^2-b^2\right)=\left(a+b+c\right)\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)\)
\(=-a^4-b^4-c^4+2a^2b^2+2b^2c^2+2a^2c^2\)
Vậy ta có BĐT cần chứng minh, đẳng thức xảy ra khi và chỉ khi \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
AD
7 tháng 6 2023
\(VT=tanA+tanB+tanC=\dfrac{sinA}{cosA}+\dfrac{sinB}{cosB}+\dfrac{sinC}{cosC}\\ =\dfrac{sinA.sinB+cosA.cosB}{cosA+cosB}+\dfrac{sinC}{cosC}\\ =\dfrac{sin\left(A+B\right)}{cosA.cosB}+\dfrac{sinC}{cosC}\)
Theo định lý tổng 3 góc trong tam giác :
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow A+B=180^o-C\\ \Leftrightarrow sin\left(A+B\right)=sin\left(180^o-C\right)=sinC\\ =\dfrac{sinC}{cosAcosB}+\dfrac{sinC}{cosC}\\ =\dfrac{sinC}{cosAcosBcosC}\left(cosC+cosAcosB\right)\\ =\dfrac{sinC}{cosAcosBcosC}\left(-cos\left(A+B\right)+cosAcosB\right)\\ =\dfrac{sinC}{cosAcosBcosC}\left(-cosAcosB+sinAsinB+cosAcosB\right)\\ =\dfrac{sinAsinBsinC}{cosAcosBcosC}\\ =\dfrac{sinA}{cosA}.\dfrac{sinB}{cosB}.\dfrac{sinC}{cosC}=tanA.tanB.tanC=VP\left(đpcm\right)\)
CM
8 tháng 10 2019
Đáp án B
Theo giả thiết có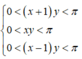 
và
Và thay vào đẳng thức điều kiện có:
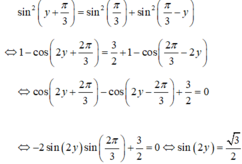
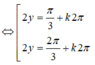
Đối chiếu với điều kiện nhận 
NT
1
UK
3 tháng 3 2019
\(\Rightarrow \tan A+\tan C=2\tan B\)
\(\Leftrightarrow \frac{\sin\left ( A+C \right )}{\cos A\cos C}=2\cdot\frac{\sin\left ( A+C \right )}{\cos B}\\\)
\(\Rightarrow \cos B=2\cos A\cos C\)
\(\Leftrightarrow 2\cos B=\cos(A-C)\)
\(\left (\cos A+\cos C \right )^2=\cos^2 A+\cos^2 C+2\cos A\cos C\\=\frac{\cos2A+\cos2C}{2}+1+\cos B\\=-\cos(B)\cos(A-C)+1+\cos B \\=-2\cos^2B+\cos B+1 \le \frac{9}{8}\\\Rightarrow \cos A+\cos C\le \frac{3\sqrt2}{4}\)
Chứng minh hoàn tất.
15 tháng 10 2017
mình làm cách này là cách khj nào mà ko cách nào khác ms làm vậy thôi, áp dụng định lí sin và cosin trong tam giác
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2020
Bạn coi lại đề bài.
N,M,P,Q là các điểm trên CD, AD, SA hay trung điểm?
Vì nếu trung điểm thì làm sao thỏa mãn MD=2MC hay NA=3ND được?
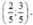
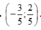
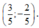
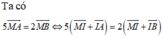
đề sai hay sao á
nếu \(\frac{tanB}{tanC}=\frac{sin^2B}{sin^2C}\) thì làm kiểu này
\(\frac{tanB}{tanC}=\frac{sin^2B}{sin^2C}=>\frac{sinB.cosC}{cosB.sinC}-\frac{sin^2B}{sin^2C}=0 \)
\(\frac{sinB}{sinC}\left(\frac{cosC}{cosB}-\frac{sinB}{sinC}\right)=0=>sinB=0\left(bỏ\right)\)
\(\frac{cosC}{cosB}-\frac{sinB}{sinC}=0=>sinC.cosC=sinB.cosB\)
\(sin2C=sin2B=>B=C\) hoặc \(\widehat{B}+\widehat{C}=\frac{\pi}{2}\)
tam giác vuông hoặc cân tại A