Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Ta có:
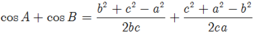
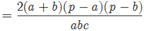
Vậy sin C = cosA + cos B khi và chỉ khi
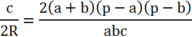
Hay ![]()
Nên c2[(a + b) 2 - c2]= (a + b)2[ c2 - (a - b)2]
Do đó; c4 = (a2 - b2) 2
Suy ra a2 = b2 + c2 hoặc b2 = c2 + a2
Suy ra; tam giác ABC vuông tại A hoặc B.

b + c = 2a
⇔ \(\dfrac{b+c}{2R}=\dfrac{2a}{2R}\) (1) với R là bán kính đường tròn ngoại tiếp
Theo định lí sin \(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}=2R\)
nên (1) ⇔ sinB + sinC = 2sinA
Chọn B

Chọn C.
Theo đầu bài ta có; b(b2 - a2) = c(c2 - a2)
Hay b3 - c3 = a2(b - c)
Mà b - c ≠ 0 nên b2 + bc + c2 = a2
Theo định lí côsin thì a2 = b2 + c2 - 2bccosA
Do đó: b2 + bc + c2 = b2 + c2 - 2bccosA
Suy ra: cos A = - ½ hay góc A bằng 1200.

Đáp án: D
a sai vì nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại A không phải vuông tại B.
b, c, d đúng.

Theo đl sin có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow b=a\dfrac{sinB}{sinA};c=\dfrac{sinC}{sinA}.a\)
Mà `b+c=2a`
\(\Rightarrow a\dfrac{sinB}{sinA}+a\dfrac{sinC}{sinA}=2a\\ \Rightarrow\dfrac{sinB}{sinA}+\dfrac{sinC}{sinA}=2\\ \Leftrightarrow sinB+sinC=2sinA\)
Chọn B

a) \(\left(P\Rightarrow Q\right)\) : " Nếu AB = AC thì tam giác ABC cân"
Mệnh đề đảo \(\left(Q\Rightarrow P\right):\)" Nếu tam giác ABC cân thì AB = AC"
b) \(\left(P\Rightarrow Q\right)\) : đúng, \(\left(Q\Rightarrow P\right):\)sai

P: “tam giác ABC vuông tại A”
Q: “tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)”
+) Mệnh đề \(Q \Rightarrow P\) là “Nếu tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\)thì tam giác ABC vuông tại A”
+) Từ định lí Pytago, ta có:
Tam giác ABC vuông tại A thì \(A{B^2} + A{C^2} = B{C^2}\)
Và: Tam giác ABC có \(A{B^2} + A{C^2} = B{C^2}\) thì vuông tại A.
Do vậy, hai mệnh đề “\(P \Rightarrow Q\)” và “\(Q \Rightarrow P\)” đều đúng.

+) Mệnh đề \(P \Rightarrow Q\) là: “Vì tam giác ABC đều nên tam giác ABC cân và có một góc bằng \({60^o}\)”.
+) Mệnh đề \(Q \Rightarrow P\) là: “Tam giác ABC cân và có một góc bằng \({60^o}\) suy ra tam giác ABC đều”.
Dễ thấy cả hai mệnh đề trên đều đúng.
+) Mệnh đề tương đương: (dùng một trong các cách sau:)
“Tam giác ABC đều tương đương tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều là điều kiện cần và đủ để có tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều khi và chỉ khi tam giác ABC cân và có một góc bằng \({60^o}\)”
“Tam giác ABC đều nếu và chỉ nếu tam giác ABC cân và có một góc bằng \({60^o}\)”
Chọn D.
+ Áp dụng định lí sin ta có
Suy ra sin2A = sinB. Sin C khi và chỉ khi :
Hay a2 = bc
+ Áp dụng định lí côsin và ý trên ta có
Vậy cả A và B đúng.