Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔHBA vuông tại B
=>HB<HA
AB<BC
=>HA<HC
=>HB<HA<HC
b: Vì HA<HC
nên góc HAC>góc HCA

a: ΔHBA vuông tại B
=>HB<HA
Vì AB<BC
nên HA<HC
=>HB<HA<HC
b: HA<HC
=>góc HCA<góc HAC
c: HA<HC
=>góc HCA<góc HAC
=>góc AHB>góc BHC

a: Xet ΔHAC có AB<BC
mà AB,BC lần lượt là hình chiếu của HA,HC trên AC
nên HA<HC
mà HB<HA
nên HB<HA<HC
b: HA<HC
=>góc HCA<góc HAC
c: góc HCA<góc HAC
=>90 độ-góc HCA>90 độ-góc HAC
=>góc BHC>góc BHA

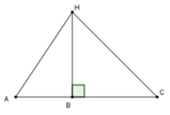
Vì BH là đường vuông góc và AH là đường xiên nên AH > BH
Chọn đáp án C.

a: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
=>ΔBAM=ΔBDM
BA=BD=3cm
CB=3+2=5cm
=>AC=4cm
AB<AC<BC
=>góc C<góc B<góc A
b: ΔBAM=ΔBDM
=>MA=MD
Xét ΔAMN vuông tại A và ΔDMC vuông tại D có
MA=MD
góc AMN=góc DMC
=>ΔAMN=ΔDMC
=>MN=MC
=>ΔMNC cân tại M

a: AC=4cm
b: Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
c: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
Do đó: ΔBAM=ΔBDM
Suy ra: MA=MD
Xét ΔAMN vuông tại A và ΔDMC vuông tại D có
MA=MD
\(\widehat{AMN}=\widehat{DMC}\)
Do đó: ΔAMN=ΔDMC
Suy ra: MN=MC
hay ΔMNC cân tại M