Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
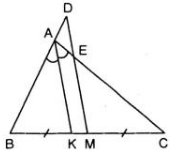
AK là đường phân giác của tam giác ABC nên:
Ta có: MD // AK
⇒ ΔABK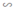 
ΔDBM và ΔECM 
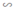ΔACK
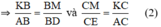
Từ (1) và (2) ta có: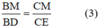 
Do BM = CM (giả thiết) nên từ (3) suy ra: BD = CE.
Bài 1:
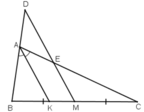
Xét tam giác $BDM$ có $AK\parallel DM$, áp dụng đl Talet:
$\frac{BA}{BD}=\frac{BK}{BM}=\frac{2BK}{BC}(*)$
Xét tam giác $CAK$ có $ME\parallel AK$, áp dụng đl Talet:
$\frac{CE}{CA}=\frac{CM}{CK}=\frac{BC}{2CK}(**)$
Lấy $(*)$ nhân $(**)$ thì:
$\frac{CE}{BD}.\frac{AB}{AC}=\frac{BK}{CK}$
Mà: $\frac{BK}{CK}=\frac{AB}{AC}$ (theo tính chất tia phân giác)
$\Rightarrow \frac{CE}{BD}=1$
$\Rightarrow CE=BD$ (đpcm)
Ta có : \(\widehat{A_1}=\widehat{A_2}\)( do \(AD\)là phân giác )
\(\widehat{K_1}=\widehat{K_2}\)( đối đỉnh )
Vì \(AD//KM\Rightarrow\widehat{A_2}=\widehat{K_1}\left(soletrong\right)\Rightarrow\widehat{A_1}=\widehat{K_1}\)
Mà \(\widehat{AEK}=\widehat{A_1}\)( cùng bù \(\widehat{DAE}\))
\(\Rightarrow\widehat{AEK}=\widehat{K_1}\Rightarrow\Delta AEK\)cân tại \(K\)
\(\Rightarrow AE=AK\)
H, K để làm gì?
Trog tg ADC có ME // AD => CM/CE = CD/CA (Ta-let) (1)
trog tg BMF có AD // MF => BM/BF = BD/BA (2)
theo t/c đường pg trog tg ABC có CD/CA = BD/BA (3)
Từ (1), (2) và (3) => CM/CE = BM/CF, mà CM = BM => CE = BF
Hồ sĩ tiến , để lm các câu a, b, c bn ak. Đây là câu cuối nhg mih o biết lm