Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a . dễ c/m được tam giác AOF đồng dạng với ADB(gg)
b. Dễ c/m được tứ giác BHKD nt do DKB=DHB=90 cùng nhìn cạnh BD
nên DHK=KBD(cùng nhìn cạnh DK)
mà DCB=DBK(cùng phụ với KBC)
từ đó ta được DHK=DCO hay tứ giác KHOC nt
c, theo mk câu c sai đề vì nếu cần c.m \(\frac{BD}{DM}-\frac{DM}{AM}=1\Leftrightarrow DB\cdot AM=DM^2+DM\cdot AM=DM\left(AM+DM\right)=DM\cdot AD\)
(đến đây vẫn đúng nha bạn)
ta thấy AMC đồng dạng với ADB hay \(\frac{AM}{AD}=\frac{MC}{DB}\Rightarrow AM\cdot BD=CM\cdot AD\)\(\Rightarrow CM\cdot AD=DM\cdot AD\Leftrightarrow CM=DM\)(vô lý )
nên mk cho là đề sai nếu mk có sai bạn chỉ mk vs ạ

a) Ax, By là các tiếp tuyến của đường tròn (O)
=> Ax // By (cùng vuông góc với AB)
=> AMNB là hình thang
Hình thang AMNB có: OA = OB; IM = IN
=> OI là đường trung bình
=> OI // AM // BN
Lại có: AM, BN vuông góc với AB
=> IO vuông góc với AB
=> AB là tiếp tuyến của đường tròn (I;IO)

d)
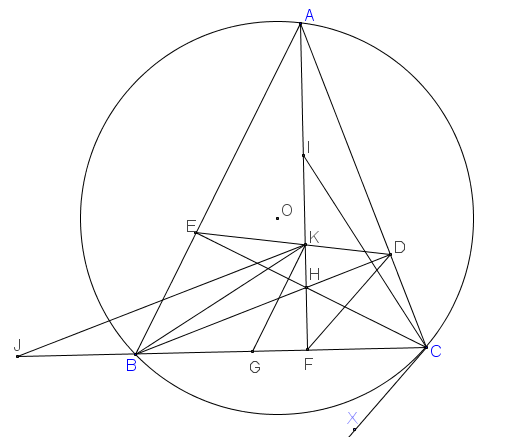
Trên BF lấy điểm G sao cho GK //AB
=>KG⊥⊥CE (1) và BGBF=AKAFBGBF=AKAF (2)
theo câu c), DH là phân giác trong ˆKDFKDF^ (3)
=>HKHF=DKDFHKHF=DKDF (4)
có DA⊥⊥DH (5)
từ (3, 5) =>DA là phân giác ngoài ˆKDFKDF^
=>AKAF=DKDFAKAF=DKDF (6)
từ (2, 4, 6) =>BGBF=HKHFBGBF=HKHF (7)
trên tia đối tia BC lấy điểm J sao cho BJ =BG
=>BJBF=BGBFBJBF=BGBF (8)
từ (7, 8) =>BJBF=HKHFBJBF=HKHF
=>JK // BH
=>JK⊥⊥AC (8)
từ (1, 8) =>ˆJKG=ˆACHJKG^=ACH^ (9)
và có JF⊥⊥AH và (1)=>ˆKGJ=ˆCHAKGJ^=CHA^ (10)
từ (9, 10) =>△KGJ∼△CHA△KGJ∼△CHA (g, g)
=>KGCH=GJHA=2.GB2.HI=GBHIKGCH=GJHA=2.GB2.HI=GBHI (11)
từ (10, 11) =>△KGB∼△CHI△KGB∼△CHI (c, g, c)
=>ˆKBF=ˆCIFKBF^=CIF^
=>△FBK∼△FIC△FBK∼△FIC (đpcm)
và ˆICB+ˆFBKICB^+FBK^
=ˆBKF+ˆFBK=90∘=BKF^+FBK^=90∘
=>BK⊥CIBK⊥CI =>K là trực tâm của tam giác IBC (đpcm)
Hình gửi kèm
ủng hộ mình nha