Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét \(\Delta ABH\) và \(\Delta MBH\) ta có:
\(\widehat{AHB}=\widehat{MHB}=90^o,AH=MH,\) cạnh chung \(BH\)
\(\Rightarrow\Delta ABH=\Delta MBH\left(c.g.c\right)\) ( ĐPCM )
b, Vì \(\Delta ABH=\Delta MBH\Rightarrow AB=MB\) ( 2 cạnh tương ứng )
\(\widehat{ABH}=\widehat{MBH}\) ( 2 góc tương ứng ) \(\Rightarrow\widehat{ABC}=\widehat{MBC}\)
Xét \(\Delta ABC\) và \(\Delta MBC\) ta có:
\(AB=MB,\widehat{ABC}=\widehat{MBC},\) cạnh chung \(BC\)
\(\Rightarrow\Delta ABC=\Delta MBC\left(c.g.c\right)\)
\(\Rightarrow\widehat{BAC}=\widehat{BMC}\) ( 2 góc tương ứng ) ( ĐPCM )
c, Xét \(\Delta AHI\) và \(\Delta MHI\) ta có:
\(AH=MH,\widehat{AHI}=\widehat{MHI}=90^o,\) cạnh chung \(HI\)
\(\Rightarrow\Delta AHI=\Delta MHI\left(c.g.c\right)\)
\(\Rightarrow AI=MI\) ( cạnh tương ứng ) \(\Rightarrow AI=NI=MI\Rightarrow AI=MI\)
\(\widehat{AIH}=\widehat{MIH}\) ( 2 góc tương ứng ) \(\Rightarrow\widehat{AIB}=\widehat{MIB}\)(1)
Vì \(\widehat{AIH}\) và \(\widehat{CIN}\) là 2 góc đối đỉnh \(\Rightarrow\widehat{AIB}=\widehat{CIN}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{MIB}=\widehat{AIB}=\widehat{CIN}\Rightarrow\widehat{MIB}=\widehat{CIN}\)
Vì I là trung điểm của BC => BI = CI
Xét \(\Delta BIM\) và \(\Delta CIN\) ta có:
\(BI=CI,\widehat{MIB}=\widehat{CIN},MI=NI\)
\(\Rightarrow\Delta BIM=\Delta CIN\left(c.g.c\right)\)
\(\Rightarrow NC=MB\) ( 2 cạnh tương ứng ) ( ĐPCM )
d, Xét tam giác vuông ABH, theo định lý Py-ta-go ta có:
\(AB^2=AH^2+BH^2\Rightarrow13^2=AH^2+12^2\Rightarrow169=AH^2+144\)
\(\Rightarrow AH^2=169-144=25\Rightarrow AH=\sqrt{25}=5\)
Xét tam giác vuông AHC, theo định lý Py-ta-go ta có:
\(AC^2=AH^2+CH^2\Rightarrow AC^2=5^2+16^2\Rightarrow AC^2=25+256\)
\(\Rightarrow AC^2=281\Rightarrow AC=\sqrt{281}\)
Vì điểm H nằm giữa điểm B và điểm C \(\Rightarrow BC=AH+CH\Rightarrow BC=12+16\Rightarrow BC=28\)

a: Xét ΔAMB và ΔNMC có
MA=MN
góc AMB=góc NMC
MB=MC
Do đó: ΔAMB=ΔNMC
b: Xét ΔBAI có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAI cân tại B
=>BA=BI=CN

#\(N\)
`a,` Xét Tam giác `AMB` và Tam giác `CME` có:
`AM = ME (g``t)`
\(\widehat{AMB}=\widehat{CME}\) `(2` góc đối đỉnh `)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `CME (c-g-c)`
`b,` Vì Tam giác `AMB =` Tam giác `CME (a)`
`-> AB = CE (2` cạnh tương ứng `)`
Xét Tam giác `ABH` và Tam giác `DBH` có:
`HA = HD (g``t)`
\(\widehat{BHA}=\widehat{BHD}=90^0\)
`BH` chung
`=>` Tam giác `ABH =` Tam giác `DBH (c-g-c)`
`=> AB = BD (2` cạnh tương ứng `)`
Mà `AB = CE -> BD = CE`
`c,` Xét Tam giác `AMH` và Tam giác `DMH` có:
`HA = HD (g``t)`
\(\widehat{AHM}=\widehat{DHM}=90^0\)
`HM` chung
`=>` Tam giác `AMH =` Tam giác `DMH (c-g-c)`
`=> AM = DM (2` cạnh tương ứng `)`
Xét Tam giác `AMD` có: `AM = DM`
`->` Tam giác `AMD` là tam giác cân.

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM

a/ Xét △ABM và △DMC có:
\(\begin{matrix}AM=MD\left(gt\right)\\MB=MC\left(gt\right)\\\hat{AMB}=\hat{CMD}\left(đối\text{ }đỉnh\right)\end{matrix}\)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\) (đpcm).
b/ Ta có: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\hat{MAB}=\hat{MDC}\); hai góc ở vị trí so le trong.
Vậy: AB // CD (đpcm).
c/ Xét △BAE có:
\(\begin{matrix}BH\perp AE\left(gt\right)\\AH=HE\left(gt\right)\end{matrix}\)
⇒ BH vừa là đường cao, vừa là đường trung tuyến.
⇒ △BAE cân tại B.
\(\Rightarrow BE=BA\). Mà \(AB=CD\left(\Delta AMB=\Delta DMC\right)\)
Vậy: BE = CD (đpcm).

Áp dụng đl Pi ta go đảo cho Tam giác ABC
=>AB2+CA2=BC2
=>152+362=392
=>1521=1521
=>Tam giác ABC vuông tại A
Áp dụng đl pi ta go cho tam giác ABH
=>AB2=AH2+BH2
=>152=92+BH2
=>BH2=225-81=144=122
=>BH=12
Vậy...

a: Xét ΔABI và ΔKCI có
IA=IK
\(\widehat{AIB}=\widehat{KIC}\)
IB=IC
Do đó: ΔABI=ΔKCI
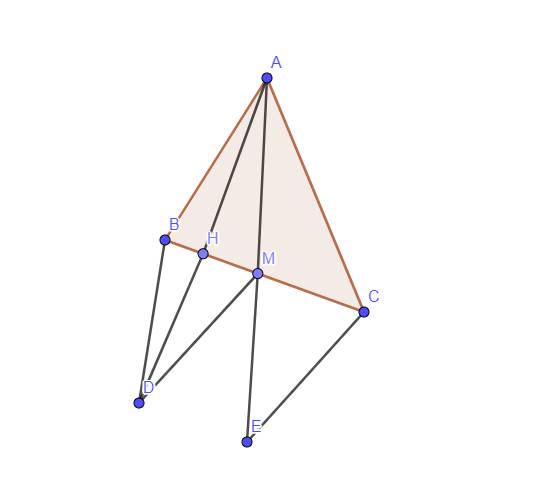
a, xét tam giác ABH và tam giác MBH có : BH chung
góc AHB = góc MHB = 90
AH = HM do H là trđ của AM
=> tam giác ABH = tam giác MBH (2cgv)
b, tam giác ABH = tam giác MBH (câu a)
=> góc ABH góc MBH (đn)
và AB= BM (đn)
xét tam giác ABC và tam giác MBC có : BC chung
=> tam giác ABC = tam giác MBC (c-g-c)
=> góc BAC = góc BMC (đn)
c, xét tam giác BIA và tam giác CIN có :
góc BIA = góc CIN (đối đỉnh)
BI = IC do I là trđ của BC (gt)
AI = IN do I là trđ của AN (gt)
=> tam giác BIA = tam giác CIN (c-g-c)
=> AB = CN (đn)
AB = MB (Câu b)
=> CN = BM
d, dùng pytago thôi