Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

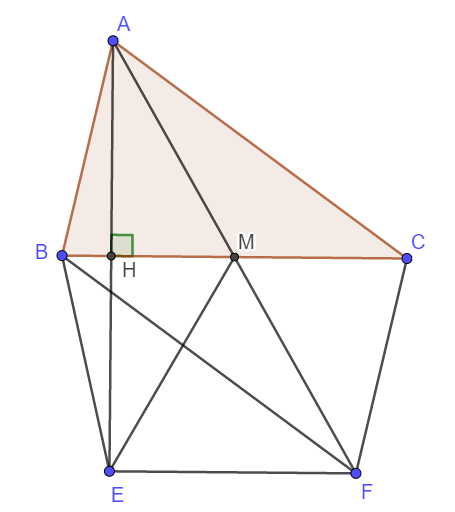
a) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên nó là tam giác cân.
Vậy thì MA = ME. Lại có MA = MF nên ME = MF.
b) Do AME là tam giác cân, MH là đường cao nên MH cũng là phân giác.
Vậy thì \(\widehat{AMB}=\widehat{BME}\)
Mà \(\widehat{AMB}=\widehat{CMF}\Rightarrow\widehat{BME}=\widehat{CMF}\)
Xét tam giác BME và CMF có:
BM = CM
ME = MF
\(\widehat{BME}=\widehat{CMF}\)
\(\Rightarrow\Delta BME=\Delta CMF\left(c-g-c\right)\)
\(\Rightarrow BE=CF\)
c) Dễ thấy \(\Delta BMF=\Delta CMA\left(c-g-c\right)\Rightarrow\widehat{BFM}=\widehat{CAM}\)
Chúng lại ở vị trí so le trong nên AC//BF.
d) Xét tam giác AEF có MA = ME = MF nên AEF là tam giác vuông. Vậy \(AE\perp EF\)
Lại có \(AE\perp BC\Rightarrow\) BC//EF

Bạn tự vẽ hình nhé!
a,chứng minh ME=MF
Xét tam giác AMH và tam giác EMH,có:
AH=HE(gt)
HM :cạnh chung
góc AHM=góc EHM=90°
=> tam giác AHM=tam giác EHM(c.g.c)
=>AM=ME (1)
Mà AM =MF (gt) (2)
Từ (1),(2) suy ra: ME=MF (t/c bắc cầu)
b,cm:BE=CF
Xét tam giác ABH và tam giác BEH,có:
AH=HE (gt)
BH cạnh chung
góc AHB=góc BHE=90°
=> tam giác BHA = tam giác EHB(c.g.c)
=>AB=BE (3)
Xét tam giác ABM và tam giác CFM,có:
BM=MC( vì M là trung điểm của BC)
AM=MF(gt)
góc AMB=góc CMF(2 góc đối đỉnh)
=> tam giác ABM = tam giác CFM(c.g.c)
=>AB=CF (4)
Từ (3),(4) suy ra: BE=CF
c,chứng minh AC//BF
Xét tam giác ACM và tam giác FBM,có:
AM=MF(gt)
BM=MC(gt)
góc AMC=góc BMF (2 góc đối đỉnh)
=> tam giác CAM = tam giác BFM (c.g.c)
=>AC=BF
=> Tứ giác ACFB có 2 cặp tam giác bằng nhau là:
Tam giác ABM= tam giác CFM
Tam giác BFM=tam giác ACM
=> BC=AF
Vì AB<AC nên tứ giác ACFB là hình chữ nhật.
=>AC//BF
d, chứng minh BC//EF
Do H và M lần lượt là trung điểm của AE va AF
AM=AF/2
AH=AE/2
HM_|_AE (gt)
=> HM là đường trung bình của tam giác AEF
=>HM//EF
Mà 2 điểm H và M nằm trên đường thẳng BC
=>BC//EF (đpcm)
Cho mình 1 K nhé!
phiền bạn có thể giải theo cách của học kì I được ko? Tại vì mình chưa học đường trung bình. Cho mình cảm ơn nhìu.
a, Bạn chứng minh : tam giác ABH=EBH ( hai cạnh góc vuông) => AB=BE
tam giác ABM=CMF ( c.g.c ) => CF=AB
=> BE=CF=AB
b, Chứng minh tam giác AHM=EHM ( hai cạnh góc vuông )
=> AM=EM mà AM=AF nên ME=MF (đpcm)